浙江省宁波市奉化区2018-2019学年九年级上学期数学期中四校联考试卷

试卷更新日期：2018-12-07 类型：期中考试

进入出卷网下载

一、选择题

1. 抛物线 $y = {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、（1，2） B、（－1，2） C、（1，－2） D、（－1，－2）

查看试题解析
2. 一个布袋里装有5个只有颜色不同的球，其中2个红球，3个白球．从布袋里任意摸出1个球，则摸出的球是红球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{5}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
3. 已知的⨀O半径为3cm，点P到圆心O的距离OP=2cm，则点P（）

A、在⨀O外 B、在⨀O 上 C、在⨀O 内 D、无法确定

查看试题解析
4. 如图，把△ABC绕点C顺时针旋转35°得到△A′B′C，A′B′交AC于点D，若A′D＝CD，则∠A的度数为（）

A、25° B、35° C、45° D、55°

查看试题解析
5. 若点A（4，y₁），B（2，y₂），C（-2，y₃）是抛物线y=（x-2）²+1上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₃＞y₁＞y₂ B、y₁＞y₃＞y₂ C、y₃＞y₂＞y₁ D、y₁＞y₂＞y₃

查看试题解析
6. 下列四个命题中，正确的有（）
①三点确定一个圆 ②平分弦的直径平分弦所对的弧
③弦长相等，则弦所对的弦心距也相等 ④相等的弧所对的圆心角相等

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 二次函数 $y = a x^{2} + b x + c$ 的x与y的部分对应值如下表：
x
-3
-2
-1
0
1
y
3
m
7
n
7
则当x=3时，y的值为（）

A、3 B、m C、7 D、n

查看试题解析
8. 已知点E在半径为5的⊙O上运动，AB是⊙O的弦且AB=8，则使△ABE的面积为8 的点E共有（）个

A、 1 B、2 C、3 D、4

查看试题解析
9. 已知，如图AB，AD是⨀O的弦，∠B=30°，点C在弦AB上，连结CO并延长交⨀O于点D，∠D=35°，则∠BAD的度数是（）

A、60° B、65° C、70° D、75°

查看试题解析
10. 函数y= $\frac{k}{x}$ 与 $y = k x^{2} - k$ （k≠0）在同一直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
11. 已知抛物线 $y = a x^{2} + b x + c (a > 0)$ 的对称轴为x=-1，交x轴的一个交点为 $(x_{1} ， 0)$ ，且 $0 < x_{1} < 1$ ，则下列结论：① $b > 0 ， c < 0$ ；② $a - b + c > 0$ ；③ $b < a$ ④ $3 a + c > 0$ ，⑤ $9 a - 3 b + c > 0$ ，其中正确的命题有（）个.

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，半径为1的⨀O与x轴负半轴，y轴正半轴分别交于点D、E，直线y=kx (k>0)交 ⨀O于A，B，AD，BE的延长线相交于点C，当k的值改变时，下列结论：①∠ACB的度数不变，②CB与CD的比值不变，③CO的长度不变．其中正确的结论的序号是（）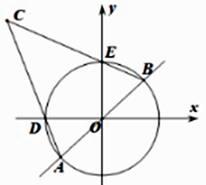

A、1 B、2 C、3 D、0

查看试题解析

二、填空题

13. 有6张卡片，每张卡片上分别写有不同的从1到6的一个自然数．从中任意抽出一张卡片，卡片上的数是3的倍数的概率是.

查看试题解析
14. 如图，AB为⨀O的弦，⨀O的半径为5，OC⊥AB于点D，交⨀O于点C，且OD=4，则弦AB的长是．

查看试题解析
15. 如图，转盘的白色扇形和黑色扇形的圆心角分别为240°和120°.让转盘自由转动2次，则指针一次落在白色区域，另一次落在黑色区域的概率是.

查看试题解析
16. 若函数 $y = a x^{2} + 3 x - 1$ 的图像与x轴有交点，则a的取值范围是．

查看试题解析
17. 如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB₁C₁D₁ ，边B₁C₁与CD交于点O，则图中阴影部分的面积为．

查看试题解析
18. 如图，一段抛物线：y=-x(x-2)（0≤x≤2）记为C₁ ，它与x轴交于两点O，A；将C₁绕点A旋转180°得到C₂ ，交x轴于A₁；将C₂绕点A₁旋转180°得到C₃ ，交x轴于点A₂ ．．．．．．如此进行下去，直至得到C₂₀₁₈ ，若点P（4035，m）在第2018段抛物线上，则m的值为．

查看试题解析

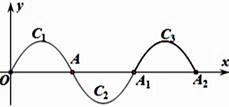
三、解答题

19. 现如今，“垃圾分类”意识已深入人心，垃圾一般可分为：可回收物、厨余垃圾、有害垃圾、其它垃圾．其中甲拿了一袋垃圾，乙拿了两袋垃圾．

(1)、直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率；

(2)、求乙所拿的两袋垃圾不同类的概率.

查看试题解析
20. 如图，二次函数的图象与x轴交于A（-3，0）和B（1，0）两点，交y轴于点C（0，3），一次函数的图象过点A、C．

(1)、求二次函数的解析式；

(2)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

查看试题解析
21. 如图，⨀O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⨀O于点D.

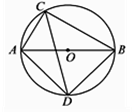(1)、求∠ADC的度数；

(2)、求弦BD的长.

查看试题解析
22. 如图，正方形网格中（每个小正方形的边长都为1个单位），在平面直角坐标系内，△OBC的顶点B、C分别为B（0，-4），C（2，-4）.

(1)、请在图中标出△OBC的外接圆的圆心P的位置，并填写：圆心P的坐标：P（，）

(2)、画出△OBC绕点O逆时针旋转90°后的△OB₁C₁ ；

(3)、在（2）的条件下，求出旋转过程中点C所经过的路径长（结果保留π）.

查看试题解析
23. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)²-4，AB为半圆的直径，求这个“果圆”被y轴截得的CD的长．

查看试题解析
24. 如图，有两面夹角为45°的墙体（∠ABC=45°）．且墙AB= $3 \sqrt{2}$ 米，墙BC=10米，小张利用8米长的篱笆围成了一个四边形菜园，如图，四边形BDEF，DE平行BC，∠E=90°（靠墙部分不使用篱笆），设EF=x，四边形面积为S．

(1)、用含x的代数式表示BD、DE的长；

(2)、求出S关于x的函数关系式，并写出x的取值范围；

(3)、求S的最大值．

查看试题解析
25. 如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，连结AC，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，连结FC．

(1)、求证：∠ACF=∠ADB；

(2)、若点A到BD的距离为m，BF+CF=n，求线段CD的长（用含m、n的代数式表示）；

(3)、当⊙P的大小发生变化而其他条件不变时， $\frac{D E}{A O}$ 的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．

查看试题解析
26. 如图，在平面直角坐标系中，已知点A的坐标 $(2 ， 4)$ ，直线 $x = 2$ 与x轴相交于点B，连结OA，抛物线 $M (1 ， 2)$ 从点O沿OA方向平移，与直线 $x = 2$ 交于点P，顶点M移动到点A时停止.

(1)、当M落在OA的中点时，则点M坐标为.

(2)、设抛物线顶点M的横坐标为m.
① 用m的代数式表示点P的坐标.
② 当m为何值时，线段PA最长?

(3)、当线段PA最长时，相应抛物线上有一点Q，使 $Δ Q M A$ 的面积与 $Δ P M A$ 的面积相等，求此时点Q的坐标.

查看试题解析