浙江省宁波市奉化区2018-2019学年八年级上学期数学期中四校联考试卷
试卷更新日期:2018-12-07 类型:期中考试
一、选择题
-
1. 下列图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长分别为3cm和2cm,则第三边长可以是( ).A、1cm B、3cm C、5cm D、7cm3. 已知直角三角形ABC,有一个锐角等于50°,则另一个锐角的度数是( ).A、30° B、 40° C、45° D、50°4. 下列句子是命题的是( )A、画∠AOB=45º B、小于直角的角是锐角吗? C、连结CD D、相等的角是对顶角5. 一元一次不等式x+1>2的解在数轴上表示为( )A、
2. 已知三角形的两边长分别为3cm和2cm,则第三边长可以是( ).A、1cm B、3cm C、5cm D、7cm3. 已知直角三角形ABC,有一个锐角等于50°,则另一个锐角的度数是( ).A、30° B、 40° C、45° D、50°4. 下列句子是命题的是( )A、画∠AOB=45º B、小于直角的角是锐角吗? C、连结CD D、相等的角是对顶角5. 一元一次不等式x+1>2的解在数轴上表示为( )A、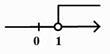 B、
B、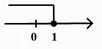 C、
C、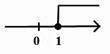 D、
D、 6. 如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )
6. 如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )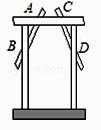 A、三角形的稳定性. B、垂线段最短. C、长方形的轴对称性. D、两点之间线段最短.7. 如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )
A、三角形的稳定性. B、垂线段最短. C、长方形的轴对称性. D、两点之间线段最短.7. 如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

A、AB=DE B、∠A=∠D C、AC=DF D、 AC∥DF8. 如图,AE⊥BC于E,BF⊥AC于F,CD⊥AB于D,△ABC中AC边上的高是线段( )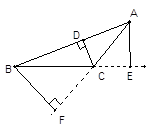 A、BF B、CD C、AE D、AF9. 已知等腰三角形的一个内角是70°,则它的顶角的度数是( )A、70° B、40° C、70°或40° D、70°或30°10. 如图,在△ABC中,边 AB的垂直平分线DE交AB于点E,交BC于点D,若BC=10,AC=6,则△ACD的周长是( )
A、BF B、CD C、AE D、AF9. 已知等腰三角形的一个内角是70°,则它的顶角的度数是( )A、70° B、40° C、70°或40° D、70°或30°10. 如图,在△ABC中,边 AB的垂直平分线DE交AB于点E,交BC于点D,若BC=10,AC=6,则△ACD的周长是( ) A、14 B、16 C、18 D、2011. 小明把一副直角三角板如图摆放,其中 ,则 等于 ( ).
A、14 B、16 C、18 D、2011. 小明把一副直角三角板如图摆放,其中 ,则 等于 ( ).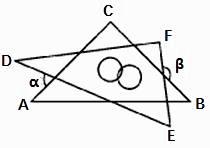 A、 B、 C、 D、12. 如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为( ).
A、 B、 C、 D、12. 如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为( ).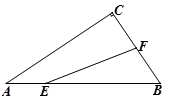 A、 B、1 C、 或1或 D、 或1或
A、 B、1 C、 或1或 D、 或1或二、填空题
-
13. 写出命题“等腰三角形两底角相等”的逆命题:.14. 若a>b,则 (填“<”或“>”).15. 直角三角形的两直角边分别是6和8,则斜边上的高线等于.16. 如图,CD是Rt△ABC斜边AB上的高,将△ACD沿CD折叠,A点恰好落在AB的中点E处,则 B等于度.
 17. 如图,在4×4方格中,点A、B在格点上,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出个.
17. 如图,在4×4方格中,点A、B在格点上,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出个.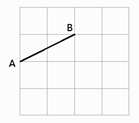 18. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.
18. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.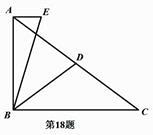
三、解答题
-
19. 解不等式组 ,并把它的解表示在数轴上.
 20. 如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF.
20. 如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF.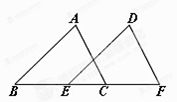
(1)、△ABC≌△DEF;
(2)、AB∥DE.
21. 如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.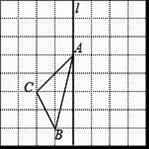
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②写出三角形ABC的面积;
③以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
④在直线l上找一点P,使PB+PC的长最短.
22. 已知,如图,四边形 , . (1)、尺规作图,在线段 上找一点 ,使得 ,连接 , (不写作法,保留作图痕迹);(2)、在(1)在图形中,若 ,且 , ,求 的长.23. 某校艺术节时欲购40盆花卉布置舞台.现有甲、乙两种花卉可供选择,已知甲种花卉的单价为18元/盆,乙种花卉的单价为25元/盆.若学校计划用于购买花卉的费用最多为860元,且购买乙花卉不少于18盆.请你为该校设计购买方案,并求出最小的费用是多少元?24. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
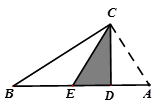
(1)、尺规作图,在线段 上找一点 ,使得 ,连接 , (不写作法,保留作图痕迹);(2)、在(1)在图形中,若 ,且 , ,求 的长.23. 某校艺术节时欲购40盆花卉布置舞台.现有甲、乙两种花卉可供选择,已知甲种花卉的单价为18元/盆,乙种花卉的单价为25元/盆.若学校计划用于购买花卉的费用最多为860元,且购买乙花卉不少于18盆.请你为该校设计购买方案,并求出最小的费用是多少元?24. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,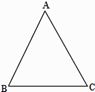 (1)、如图△ABC中,AB=AC= ,BC=2,求证:△ABC是“美丽三角形”;(2)、在Rt△ABC中,∠C=90°,AC= ,若△ABC是“美丽三角形”,求BC的长.25. 如图
(1)、如图△ABC中,AB=AC= ,BC=2,求证:△ABC是“美丽三角形”;(2)、在Rt△ABC中,∠C=90°,AC= ,若△ABC是“美丽三角形”,求BC的长.25. 如图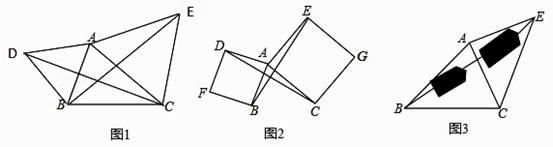 (1)、如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请猜想BE与CD的数量关系: ;你是通过证明 得到的.(2)、如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;(3)、运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
(1)、如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请猜想BE与CD的数量关系: ;你是通过证明 得到的.(2)、如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;(3)、运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.