人教版九年级数学上册 24.4 弧长和扇形面积（一） 同步练习
试卷更新日期：2018-12-06 类型：同步测试
一、选择题
-
1. 如图，AB是⊙O的直径，点D为⊙O上一点，且∠ABD=30°，BO=4，则 的长为（ ）
A、 B、 C、2π D、2. 如图，一段公路的转弯处是一段圆弧（ ），则 的展直长度为（ ）
A、3π B、6π C、9π D、12π3. 如图，在△ABC中，∠ACB=90°，∠A=30°，AB=4，以点B为圆心，BC长为半径画弧，交边AB于点D，则 的长为（ ）
A、 π B、 π C、 π D、 π4. 如图，△ABC内接于⊙O，∠A=60°，BC=6 ，则 的长为（ ）
A、2π B、4π C、8π D、12π5. 如图，⊙O的直径AB=6，若∠BAC=50°，则劣弧AC的长为（ ）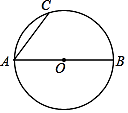
A、2π B、 C、 D、6. 如图，正方形ABCD内接于⊙O，AB=2 ，则 的长是（ ）
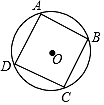A、π B、 π C、2π D、 π7. 如图，在菱形ABCD中，∠ABC=60°，AB=4，点E是AB边上的动点，过点B作直线CE的垂线，垂足为F，当点E从点A运动到点B时，点F的运动路径长为（ ）
A、 B、2 C、 π D、 π二、填空题
-
8. 一个扇形的圆心角为120°，它所对的弧长为6πcm，则此扇形的半径为cm．9. 如图，圆锥侧面展开得到扇形，此扇形半径 CA=6，圆心角∠ACB=120°， 则此圆锥高 OC 的长度是 ．
10. 如图，△ABC是⊙O的内接三角形，∠BAC=60°， 的长是 ，则⊙O的半径是 ．
11. 如图，△ABC的外接圆O的半径为3，∠C=55°，则劣弧 的长是 ． （结果保留π）
12. 如图，在平面直角坐标系中，已知点A（1，1），以点O为旋转中心，将点A逆时针旋转到点B的位置，则 的长为 ．
13. 如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，∠AOB=120°，从A到B只有路 ，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB．通过计算可知，这些市民其实仅仅少走了步（假设1步为0.5米，结果保留整数）．（参考数据： ≈1.732，π取3.142）
三、解答题
-
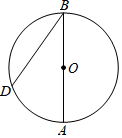
14. 如图，AB为⊙O的直径，点C在⊙O外，∠ABC的平分线与⊙O交于点D，∠C=90°．
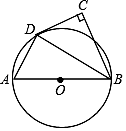(1)、CD与⊙O有怎样的位置关系？请说明理由；(2)、若∠CDB=60°，AB=6，求 的长．15. 如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E．点C是弧BF的中点．
(1)、求证：AD⊥CD；(2)、若∠CAD=30°．⊙O的半径为3，一只蚂蚁从点B出发，沿着BE--EC--弧CB爬回至点B，求蚂蚁爬过的路程(π≈3.14， ≈1.73，结果保留一位小数．)16. 如图，在△ABC中，以AB为直径的⊙O分别于BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F．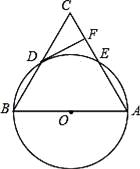
(1)、求证：DF⊥AC；(2)、若⊙O的半径为5，∠CDF=30°，求 的长（结果保留π）．17. 如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E， =
(1)、求证：OA=OB；(2)、已知AB=4 ，OA=4，求阴影部分的面积．
