人教版九年级数学上册 24.3 正多边形和圆 同步练习
试卷更新日期：2018-12-06 类型：同步测试
一、选择题
-
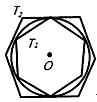
1. 正三角形的外接圆半径与内切圆的半径之比是（ ）A、1：2 B、1： C、：1 D、2：12. 已知某个正多边形的内切圆的半径是 ， 外接圆的半径是2，则此正多边形的边数是（ ）A、八 B、六 C、四 D、三3. 已知圆的半径是2 ，则该圆的内接正六边形的面积是（ ）
A、3 B、9 C、18 D、364.顺次连接正六边形的三个不相邻的顶点，得到如图的图形，下列说法错误的是（ ）
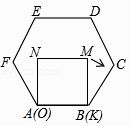
A、△ACE是等边三角形 B、既是轴对称图形也是中心对称图形 C、连接AD，则AD分别平分∠EAC与∠EDC D、图中一共能画出3条对称轴5. 下列正多边形中，中心角等于内角的是( ).A、正三角形 B、正四边形 C、正六边形 D、正八边形6. 半径为8cm的圆的内接正三角形的边长为（ ）A、 cm B、 cm C、8cm D、4cm7. 已知正方形MNOK和正六边形ABCDEF边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示，按下列步骤操作：将正方形在正六边形中绕点B顺时针旋转，使KM边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使MN边与CD边重合，完成第二次旋转；…在这样连续6次旋转的过程中，点B，M间的距离可能是（ ）
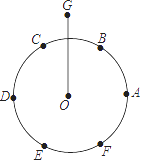
A、1.4 B、1.1 C、0.8 D、0.58. 尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（ ）
A、 r B、（1+ ）r C、（1+ ）r D、 r二、填空题
-
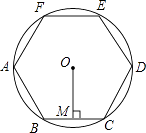
9. 如图，正六边形ABCDEF内接于⊙O，⊙O的半径为6，则这个正六边形的边心距OM的长为 ．
10. 如图，在边长为2的正八边形中，把其不相邻的四条边均向两边延长相交成一个四边形ABCD，则四边形ABCD的周长是 ．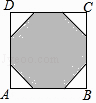
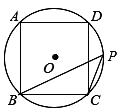
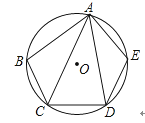
11.如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，则∠B+∠E= .
12. 刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积，设圆O的半径为1，若用圆O的外切正六边形的面积S来近似估计圆O的面积，则S= ． （结果保留根号）13. 同一个圆的内接正方形和正三角形的边心距的比为 ．14. 如图，P、Q分别是⊙O的内接正五边形的边AB、BC上的点，BP=CQ，则∠POQ= ．
15. 如图，正六边形ABCDEF的边长是6+4 ，点O1 ， O2分别是△ABF，△CDE的内心，则O1O2= ．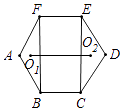
三、解答题
-
16. 如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．
17. 如图，正六边形ABCDEF内接于⊙O，若⊙O的内接正三角形ACE的面积为48 ，试求正六边形的周长．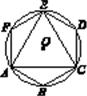
18. 尺规作图：如图，AC为⊙O的直径．
(1)、求作：⊙O的内接正方形ABCD．（要求：不写作法，保留作图痕迹）；
(2)、当直径AC=4时，求这个正方形的边长．
