人教版九年级数学上册 24.2.2 直线和圆的位置关系(五) 同步练习
试卷更新日期:2018-12-06 类型:同步测试
一、选择题
-
1. 在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )A、1.5,2.5 B、2,5 C、1,2.5 D、2,2.52. 如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )
 A、55° B、60° C、65° D、70°3. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
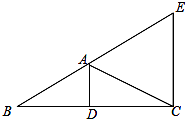
A、55° B、60° C、65° D、70°3. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )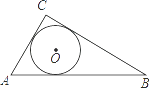 A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点4. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点4. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) A、240° B、360° C、480° D、540°5. 已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )A、 B、 C、 D、6. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A、240° B、360° C、480° D、540°5. 已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )A、 B、 C、 D、6. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )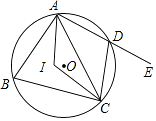 A、56° B、62° C、68° D、78°7. 如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
A、56° B、62° C、68° D、78°7. 如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( ) A、2 B、3 C、 D、8. 如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A、2 B、3 C、 D、8. 如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )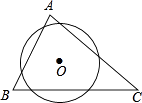 A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形
A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形二、填空题
-
9. 直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .10. 已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.11. 在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为12. 在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .13. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .
 14. 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=度.
14. 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=度.
三、解答题
-
15. Rt△ABC中,∠C=90°,AC=6,BC=8.求△ABC的内切圆半径 .
 16. 如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.
16. 如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点. (1)、求证:四边形ODCE是正方形;(2)、如果AC=6,BC=8,求内切圆⊙O的半径.
(1)、求证:四边形ODCE是正方形;(2)、如果AC=6,BC=8,求内切圆⊙O的半径.