人教版九年级数学上册 24.2.2 直线和圆的位置关系（三） 同步练习
试卷更新日期：2018-12-06 类型：同步测试
一、选择题
-
1. 下列说法正确的是（ ）A、垂直于半径的直线是圆的切线 B、圆周角等于圆心角的一半 C、圆是中心对称图形 D、圆的对称轴是直径2. 如L是⊙O的切线，要判定AB⊥L，还需要添加的条件是（ ）A、AB经过圆心O B、AB是直径 C、AB是直径，B是切点 D、AB是直线，B是切点3. 已知⊙O的半径为5，直线EF经过⊙O上一点P（点E，F在点P的两旁），下列条件能判定直线EF与⊙O相切的是（ ）
A、OP=5 B、OE=OF C、O到直线EF的距离是4 D、OP⊥EF4.如图，AB是⊙O的直径，下列条件中不能判定直线AT是⊙O的切线的是（ ）
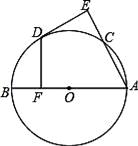
A、AB=4，AT=3，BT=5 B、∠B=45°，AB=AT C、∠B=55°，∠TAC=55° D、∠ATC=∠B5. 如图，AB是⊙O的弦，半径OC经过AB的中点D，CE∥AB，点F在⊙O上，连接CF，BF，下列结论中，不正确的是（ ）
A、∠F= B、AB⊥BF C、CE是⊙O的切线 D、6. 如图，在⊙O中，E是半径OA上一点，射线EF⊥OA，交圆于B，P为EB上任一点，射线AP交圆于C，D为射线BF上一点，且DC=DP，下列结论：①CD为⊙O的切线；②PA＞PC；③∠CDP=2∠A，其中正确的结论有（ ）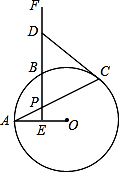
A、3个 B、2个 C、1个 D、0个7. 如图，在直角坐标系中，⊙O的半径为1，则直线y=﹣2x+ 与⊙O的位置关系是（ ）
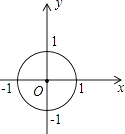A、相离 B、相交 C、相切 D、无法确定8. 如图，P为圆O外一点，OP交圆O于A点，且OA=2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：（甲）以P为圆心，OP长为半径画弧，交圆O于B点，则直线PB即为所求；
（乙）作OP的中垂线，交圆O于B点，则直线PB即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）
A、两人皆正确 B、两人皆错误 C、甲正确，乙错误 D、甲错误，乙正确二、填空题
-
9. 如图，点A、B、D在⊙O上，∠A=25°，OD的延长线交直线BC于点C，且∠OCB=40°，直线BC与⊙O的位置关系为 ．
10. 如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为 ．
11. 如图，在△ABC中，AB=AC，∠B=30°，以点A为圆心，以3cm为半径作⊙A，当AB=cm时，BC与⊙A相切．
12. 如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向以0.5个单位/秒的速度平移，使⊙P与y轴相切，则平移的时间为秒．
13. 如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O的切线，需添加的条件是 ． （不添加其他字母和线条）
14. 已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为 ．三、解答题
-
15. 如图，AB是⊙O的弦，OC⊥OA，交AB与点P，且PC=BC，求证：BC是⊙O的切线．
16. 如图，CD是⊙O的直径，并且AC=BC，AD=BD．求证：直线AB是⊙O的切线．
17. 如图，P是∠BAC的平分线上一点，PD⊥AC，垂足为D，AB与以P为圆心、PD为半径的圆相切吗？请说明理由．
18. 如图，AB是⊙O的直径，C为⊙O上一点，MN过C点，AD⊥MN于D，AC平分∠DAB．求证：MN为⊙O的切线．
