浙江省杭州市萧山区戴村片2017届九年级3月联考数学试卷
试卷更新日期:2017-03-28 类型:月考试卷
一、选择题
-
1. 实数 的值在( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间2.
三本相同的书本叠成如图所示的几何体,它的主视图是( )
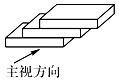 A、
A、 B、
B、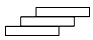 C、
C、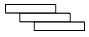 D、
D、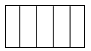 3. 下列运算正确的是( )A、2a3•a4=2a7 B、a3+a4=a7 C、(2a4)3=8a7 D、a3÷a4=a4. 一个不透明的袋子中有2个白球,3个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
3. 下列运算正确的是( )A、2a3•a4=2a7 B、a3+a4=a7 C、(2a4)3=8a7 D、a3÷a4=a4. 一个不透明的袋子中有2个白球,3个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
A、 B、 C、 D、5. 某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A、最高分 B、中位数 C、方差 D、平均数6. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )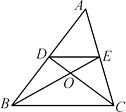 A、DE是△ABC的中位线 B、点O是△ABC的重心 C、△DEO∽△CBO D、=7. 已知关于x的方程x2+ax+b+1=0的解为x1=x2=2,则a+b的值为( )A、-3 B、-1 C、1 D、78. 若方程组 的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )A、3 B、2 C、6 D、79. 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )
A、DE是△ABC的中位线 B、点O是△ABC的重心 C、△DEO∽△CBO D、=7. 已知关于x的方程x2+ax+b+1=0的解为x1=x2=2,则a+b的值为( )A、-3 B、-1 C、1 D、78. 若方程组 的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )A、3 B、2 C、6 D、79. 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )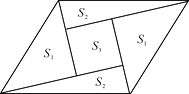 A、4S1 B、4S2 C、4S2+S3 D、3S1+4S310. 已知抛物线 ( < <0)与x轴最多有一个交点,现有以下结论:
A、4S1 B、4S2 C、4S2+S3 D、3S1+4S310. 已知抛物线 ( < <0)与x轴最多有一个交点,现有以下结论:① <0;②该抛物线的对称轴在y轴左侧;③关于x的方程 有实数根;④对于自变量x的任意一个取值,都有 ,其中正确的为( )
A、①② B、①②④ C、①②③ D、①②③④二、填空题
-
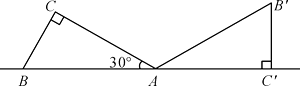
11. 已知 = ,则 = .12. 计算: = .13. 如图所示,将一个含30°角的直角三角板ABC绕点A顺时针旋转,使得点B,A,C′在同一条直线上,若BC=1,则点B旋转到B′所经过的路线长为 .
 14. 已知关于x的方程 =2的解是负数,则n的取值范围为 .15. 平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .16. 在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .
14. 已知关于x的方程 =2的解是负数,则n的取值范围为 .15. 平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .16. 在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .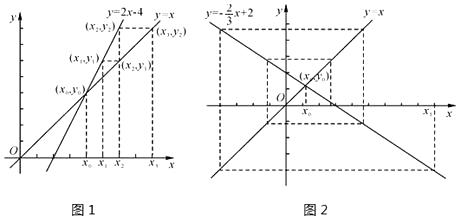
三、解答题
-
17. 按要求完成下面两个小题:
(1)、计算:( - + )÷(- )
(2)、分解因式:x3-4x18. 如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30º,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45º,请计算旗杆AB的高度(结果保留根号) .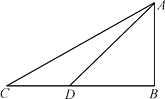 19. 有一种用“☆”定义的新运算:对于任意实数a,b都有a☆b=b2+a.例如7☆4=42+7=23.(1)、已知m☆2的结果是6,则m的值是多少?(2)、将两个实数n和n+2用这种新定义“☆”加以运算,结果为4,则n的值是多少?20. 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
19. 有一种用“☆”定义的新运算:对于任意实数a,b都有a☆b=b2+a.例如7☆4=42+7=23.(1)、已知m☆2的结果是6,则m的值是多少?(2)、将两个实数n和n+2用这种新定义“☆”加以运算,结果为4,则n的值是多少?20. 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
分数段
频数
频率
80≤x<85
a
0.2
85≤x<90
80
b
90≤x<95
60
c
95≤x<100
20
0.1
(1)、求出表中a,b,c的数值,并补全频数分布直方图;(2)、获奖成绩的中位数落在哪个分数段?(3)、估算全体获奖同学成绩的平均分.21. 如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= .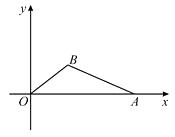 (1)、在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)(2)、求点B的坐标与cos∠BAO的值;(3)、若A,O位置不变,将点B沿 x 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.22. 在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.
(1)、在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)(2)、求点B的坐标与cos∠BAO的值;(3)、若A,O位置不变,将点B沿 x 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.22. 在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.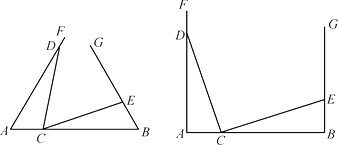
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60º或∠FAB=∠GBA=90º两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
23. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)、求抛物线的顶点坐标.(2)、AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)、若横、纵坐标都是整数的点叫整点.①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.