江西省赣州市2018-2019学年上学期七年级数学第三章单元测试-在线组卷题库

1. 若x=﹣3是方程2（x﹣m）=6的解，则m的值为（）

A、6 B、﹣6 C、12 D、﹣12

查看试题解析
2. 下列等式变形：①如果x=y，那么ax=ay；②如果x=y，那么 $\frac{x}{a} = \frac{y}{a}$ ；③如果ax=ay，那么x=y；④如果 $\frac{x}{a} = \frac{y}{a}$ ，那么x=y．其中正确的是（）

A、③④ B、①② C、①④ D、②③

查看试题解析
3. 下列方程中：①x²-1=x+3；②x-1=2；③2²+3²=13；④x-3；⑤x+y=6．其中是一元一次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若（m-2）x^|2m-3|=6是关于x的一元一次方程，则m的值是（）

A、1 B、任何数 C、2 D、1或2

查看试题解析
5. 把1400元的奖金按两种奖给22名学生，其中一等奖每人200元，二等奖每人50元，设获一等奖的学生有x人，则下列方程错误的是（）

A、200x+50（22-x）=1400 B、 $\frac{1400 - 200 x}{50} + x = 22$ C、50x+200×（22-x）=1400 D、（200-50）x+50×22=1400

查看试题解析
6. 将方程 $0.9 + \frac{0.5 x - 0.2}{0.2} = \frac{1.5 - 5 x}{0.5}$ 变形正确的是（）

A、9+ $\frac{5 x - 2}{2} = \frac{15 - 50 x}{5}$ B、0.9+ $\frac{5 x - 2}{2} = \frac{15 - 5 x}{5}$ C、9+ $\frac{5 x - 2}{2} = \frac{15 - 5 x}{5}$ D、0.9+ $\frac{5 x - 2}{2}$ =3﹣10x

查看试题解析

7. 小明在做解方程的作业时，不小心将方程中的一个常数污染得看不清楚，方程是： $2 y + \frac{1}{2} = - y -$ ．小明翻看了书后的答案，此方程的解是y= $- \frac{1}{2}$ ，则这个常数是．

查看试题解析
8. 若关于x的方程 $(m - 2) x^{| m | - 1} = 5$ 是一元一次方程，则m的值为．

查看试题解析
9. 已知关于 $x$ 的方程 $4 x + 2 m = 3 x + 1$ 与方程 $3 x + 2 m = 6 x + 1$ 的解相同，则方程的解为.

查看试题解析
10. 若单项式3ac^x+2与-7ac^2x-1是同类项，可以得到关于x的方程为．

查看试题解析
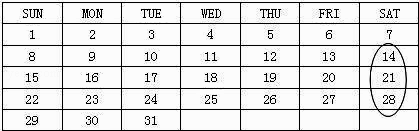
11. 如图是2005年5月份的日历，如图中那样，用一个圈竖着圈住3个数，如果被圈住的三个数的和为30，则这三个数最小一个所表示的日期为2005年5月日．

查看试题解析
12. 规定一种运算“*”，a*b= $\frac{1}{3}$ a﹣ $\frac{1}{4}$ b，则方程x*2=1*x的解为．

查看试题解析

13. 解方程：

(1)、6x+2(2-2x)=-2

(2)、 $\frac{2 x - 1}{4} = 1 - \frac{x + 2}{3}$

查看试题解析
14. 已知关于x的方程 $\frac{x + 2}{3} - 1 = \frac{k - 7}{6} - \frac{x}{2}$ 的解是x=-2，求k的值．

查看试题解析
15. 关于x的方程（a²-1）x²+（a-1）x+4a-2=0是一元一次方程，求a的值．

查看试题解析
16. 已知关于x的方程 $\frac{x - m}{2} = x + \frac{m}{3}$ 与 $\frac{x + 1}{2}$ =3x﹣2的解互为相反数，求m的值．

查看试题解析
17. 已知关于 $x$ 的方程 $m x + 2 = 2 (m - x)$ 的解满足 $| x - \frac{1}{2} | - 1 = 0$ ，则 $m$ 的值．

查看试题解析

江西省赣州市2018-2019学年上学期七年级数学第三章单元测试

购买苹果（千克）	不超过20千克	20千克以上但不超过40千克	40千克以上
每千克的价格	6元	5元	4元