江苏省无锡市锡北片2018-2019学年七年级上学期数学期中考试试卷
试卷更新日期:2018-12-04 类型:期中考试
一、单选题
-
1. ﹣5的相反数是( )A、 B、﹣5 C、﹣ D、52. 在实数:﹣(﹣3.14159),1.010010001…,﹣(﹣1)2013 , , , , 中,分数有( )A、1个 B、2个 C、3个 D、4个3. 下列各式符合代数式书写规范的是( )A、a8 B、m﹣1元 C、 D、1x4. 在代数式 ,0,1-3a, , , 中,整式有( ).
A、3个 B、4个 C、5个 D、6个5. 用代数式表示“a与b的2倍的差的平方”,正确的是( )A、2(a﹣b)2 B、(a﹣2b)2 C、a﹣2b2 D、a﹣(2b)26. 对有理数a、b,规定运算如下:a※b=a+ab , 则﹣2※3的值为( )A、﹣10 B、﹣8 C、﹣6 D、﹣47. 若a,b互为相反数,c,d互为倒数, ,则 的值为( ).A、4 B、—3 C、1 D、—3或18. 下面计算正确的是( )A、6a-5a=1 B、a+2a2=3a2 C、-(a-b)=-a+b D、2(a+b)=2a+b9. 小惠在纸上画了一条数轴后,折叠纸面,使数轴上表示l的点与表示-3的点重合,若数轴上A,B两点之间的距离为8(A在B的左侧),且A,B两点经上述折叠后重合,则A点表示的数为( )A、-4 B、-5 C、-3 D、-210. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 的值为( )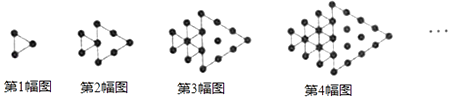 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
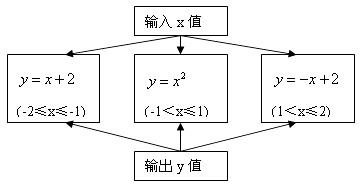
11. ﹣3 的绝对值为 , 的倒数为 .12. 单项式﹣ πxy2的系数是 , 多项式3x3y﹣2x2y2+5xy﹣1是次项式.13. 我国拟设计建造的长江三峡电站,估计总装机容量将达16780000千瓦,用科学记数法表示总装机容量是。14. 如果数轴上的A点所表示的数是﹣3,那么数轴上与点A的距离等于5个单位的点所表示的数是 .15. 已知代数式 的值为2,则代数式3x2﹣4x﹣7的值为 .16. 根据图示的程序计算函数值,若输入的x的值为 ,则输出的结果为
 17. 若代数式﹣2a3bm与3an+1b4是同类项,则mn= .18. 当k=时,多项式 中不含xy项.19. 开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为元.20. 有理数a、b、c在数轴上的位置如图:
17. 若代数式﹣2a3bm与3an+1b4是同类项,则mn= .18. 当k=时,多项式 中不含xy项.19. 开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为元.20. 有理数a、b、c在数轴上的位置如图: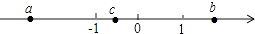 (1)、用“>”或“<”填空:b+c0;b﹣a0;a+c0;(2)、化简|b+c|+|b﹣a|﹣|a+c|.
(1)、用“>”或“<”填空:b+c0;b﹣a0;a+c0;(2)、化简|b+c|+|b﹣a|﹣|a+c|.三、解答题
-
21.(1)、计算:
①﹣12+15﹣|﹣7﹣8|
②(﹣3)×(﹣9)﹣(﹣5)
③
④
(2)、化简:①
②7a+3(a-3b)-2(b-3a)
22. 化简求值:求代数式7a2b+2(2a2b﹣3ab2)﹣3(4a2b-ab2)的值,其中a,b满足|a+2|+(b﹣ )2=0.23. 已知代数式A=2x2+3xy+2y-1,B=x2-xy+x- , x-y=-1,xy=1(1)、求A-2B;(2)、若A-2B的值与x的取值无关,求y的值.24. 民谚有云:“不到庐山辜负目,不食螃蟹辜负腹.”,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.B家的规定如下表:
数量范围
(千克)
0~50部分
(含50)
50以上~150部分(含150,不含50)
150以上~250部分(含250,不含150)
250以上部分
(不含250)
价 格(元)
零售价的95%
零售价的85%
零售价的75%
零售价的70%
(1)、如果他批发90千克太湖蟹,则他在A家批发需要元,在B家批发需要元;(2)、如果他批发x千克太湖蟹(150<x<200),则他在A家批发需要元,在B家批发需要元(用含x的代数式表示);(3)、现在他要批发170千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.25. 结合数轴与绝对值的知识回答下列问题:(1)、探究:①数轴上表示5和2的两点之间的距离是多少.
②数轴上表示﹣2和﹣6的两点之间的距离是多少.
③数轴上表示﹣4和3的两点之间的距离是多少.
(2)、归纳:一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.
②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.
③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.
 (3)、拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1 , A2 , A3 , A4 , A5 , …A2014 , 某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.
(3)、拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1 , A2 , A3 , A4 , A5 , …A2014 , 某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.