江苏省无锡市东林集团2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2018-12-04 类型：期中考试

进入出卷网下载

一、单选题

1. 比2℃低8℃的温度是（）

A、﹣8℃ B、8℃ C、6℃ D、－6℃

查看试题解析
2. 下列计算正确的是（）

A、 $2^{3}$ =6 B、－ $4^{2}$ =－16 C、－8－8=0 D、－5－2=－7

查看试题解析
3. 下列运算，结果正确的是（）

A、2ab－2ba=0 B、2a²+3a²=6a² C、3xy－4xy=－1 D、2x³+3x³=5x⁶

查看试题解析
4. 在下面各数中有理数的个数有（）
－3.14， $\frac{22}{7}$ ，0.1010010001，+1.99， $- \frac{π}{3}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 某品牌电脑原价为m元，先降价n元，又降价20%后售价为（）

A、0.8（m＋n）元 B、0.8（m－n）元 C、0.2（m＋n）元 D、0.2（m－n）元

查看试题解析
6. 下列各数－6.1，－ $| + \frac{1}{2} |$ ，－（－1），－2² ， (－2)³ ， $- [- (- 3)]$ 中，负数的个数有（）

A、3 B、4 C、5 D、6

查看试题解析
7. 下列说法错误的是（）

A、 $\frac{π x}{5}$ 的系数是 $\frac{1}{5}$ B、 $\frac{3 x - 1}{3}$ 是多项式 C、 $- 2^{5} m$ 的次数是1 D、 $- x^{2} y - 3^{5} x y^{3}$ 是四次二项式

查看试题解析
8. 已知 $a ， b$ 两数在数轴上的位置如图所示，则化简代数式 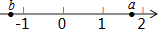$| a + b | - | a - 1 | + | b + 2 |$ 的结果是（）

A、1 B、 $2 a - 3$ C、2b+3 D、－1

查看试题解析
9. 已知 $m^{2} + 2 m n = 13$ ， $3 m n + 2 n^{2} = 21$ ，则 $2 m^{2} + 13 m n + 6 n^{2} - 44$ 的值为（）

A、45 B、55 C、65 D、75

查看试题解析
10. a是不为2的有理数，我们把 $\frac{2}{2 - a}$ 称为a的“哈利数”。如：3的“哈利数”是 $\frac{2}{2 - 3} = - 2$ ，－2的“哈利数”是 $\frac{2}{2 - (- 2)} = \frac{1}{2}$ ，已知 $a_{1} = 3$ ， $a_{2}$ 是 $a_{1}$ 的“哈利数”， $a_{3}$ 是 $a_{2}$ 的“哈利数”， $a_{4}$ 是 $a_{3}$ 的“哈利数”，…，依次类推，则 $a_{2018}$ =（）。

A、3 B、－2 C、 $\frac{1}{2}$ D、 $\frac{4}{3}$

查看试题解析

二、填空题

11. “辽宁号”航空母舰的满载排水量为67500吨，将数67500用科学记数法表示为．

查看试题解析
12. －3的绝对值是．

查看试题解析
13. 若关于的方程 $2 x - k + 4 = 0$ 的解是x=3，那么k的值是．

查看试题解析
14. 比较大小： $- \frac{5}{6}$ $- \frac{7}{8}$ .（填“＞”、“=”、“＜”号）．

查看试题解析
15. 已知 $4 x^{2 m} y^{m + n}$ 与 $3 x^{6} y^{2}$ 是同类项，则m－n= ．

查看试题解析
16. 已知方程 $（ m - 3) x^{| m - 2 |} + 4 = 2 m$ 是关于 $x$ 的一元一次方程，则 $m$ = ．

查看试题解析
17. 在智力竞赛中，主持人问这样一道题目：“a是最小的正整数，b是最大的负整数，c是绝对值最小的有理数，请问：a，b，c三数之和是． ”

查看试题解析
18. 按下面的程序计算，若开始输入的值x为正数，最后输出的结果为15，则满足条件的x的值有．

查看试题解析

三、解答题

19. －4，|－2|，－2，－（－3.5），0，－ $1 \frac{1}{2}$

(1)、在如图所示的数轴上表示出以上各数；

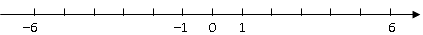(2)、比较以上各数的大小，用“＜”号连接起来；

查看试题解析
20. 计算或化简：

(1)、 $- 8 - (- 15) + (- 9) - (- 12)$

(2)、 $(- 1 \frac{1}{2}) + 1.25 + (- 8.5) + 10.75$

(3)、4×(－ $\frac{2}{5}$ )+(－2)²×5－4÷(－ $\frac{5}{12}$ )；

(4)、 $[- 2^{2} - (\frac{7}{9} - \frac{11}{12} + \frac{1}{6}) \times 36] \div 5$

(5)、 $2 a b - 3 a - \frac{1}{3} + 2 a - 2 a b + 1$

(6)、 $5 (3 a^{2} b - a b^{2}) - 4 (- a b^{2} + 3 a^{2} b)$

查看试题解析
21. 解方程：

(1)、3x－4(x+1)=1

(2)、 $\frac{x - 3}{2}$ － $\frac{2 x + 1}{3}$ =1

查看试题解析
22. 先化简再求值：
$3 x^{2} y - [3 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y) + x y] + 3 x y^{2}$ ，其中 $x = 3$ ， $y = - \frac{1}{3}$ ．

查看试题解析
23. 某商场将进货价为40元的台灯以50元的销售价售出，平均每月能售出800个．市场调研表明：当销售价每上涨1元时，其销售量就将减少10个．若设每个台灯的销售价上涨 $a$ 元．

(1)、试用含 $a$ 的代数式填空：
①涨价后，每个台灯的销售价为元；
②涨价后，商场的台灯平均每月的销售量为台；
③涨价后，商场每月销售台灯所获得总利润为元．

(2)、如果商场要想销售总利润平均每月达到20000元，商场经理甲说“在原售价每台50元的基础上再上涨40元，可以完成任务”，商场经理乙说“不用涨那么多，在原售价每台50元的基础上再上涨30元就可以了”，试判断经理甲与乙的说法是否正确，并说明理由．

查看试题解析
24.

(1)、在下列横线上用含有a，b的代数式表示相应图形的面积．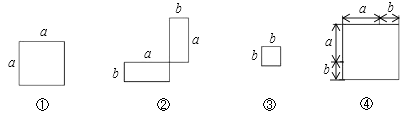

①a²；②；③b²；④.

(2)、请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达：．

(3)、利用（2）的结论计算10.23²+20.46×9.77+9.77²的值．

查看试题解析
25. 已知数轴上有A、B、C三点，分别表示有理数－26、－10、10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．

(1)、用含t的代数式表示P到点A和点C的距离：PA= ， PC=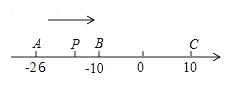

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后，请用t的代数式表示P、Q两点间的距离。（友情提醒：注意考虑P、Q的位置）

查看试题解析