人教版九年级数学上册 24.2.1 点和圆的位置关系(一) 同步练习
试卷更新日期:2018-12-04 类型:同步测试
一、选择题.
-
1. 已知☉O的半径为6,A为线段PO的中点,当OP=10时,点A与☉O的位置关系为( )A、在圆上 B、在圆外 C、在圆内 D、不确定2. 如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在 外, 内, 上,则原点O的位置应该在( )
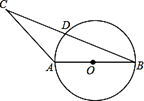
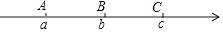 A、点A与点B之间靠近A点 B、点A与点B之间靠近B点 C、点B与点C之间靠近B点 D、点B与点C之间靠近C点3. 若点A的坐标为(3,4),⊙A的半径5,则点P(6,3)的位置为( )A、P在⊙A内 B、P在⊙A上 C、P在⊙A外 D、无法确定4. 已知 的半径为 , 为圆外一点, 为线段 的中点,当 时,点 和 的位置关系是( )A、点A在⊙O内 B、点A在⊙O外 C、点A在⊙O上 D、无法确定5. 已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,PA= , 那么点P与⊙O的位置关系是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定6. 用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )A、点在圆内 B、点在圆上 C、点在圆心上 D、点在圆上或圆内7. 如图,在Rt△ABC中∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是( )
A、点A与点B之间靠近A点 B、点A与点B之间靠近B点 C、点B与点C之间靠近B点 D、点B与点C之间靠近C点3. 若点A的坐标为(3,4),⊙A的半径5,则点P(6,3)的位置为( )A、P在⊙A内 B、P在⊙A上 C、P在⊙A外 D、无法确定4. 已知 的半径为 , 为圆外一点, 为线段 的中点,当 时,点 和 的位置关系是( )A、点A在⊙O内 B、点A在⊙O外 C、点A在⊙O上 D、无法确定5. 已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,PA= , 那么点P与⊙O的位置关系是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定6. 用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )A、点在圆内 B、点在圆上 C、点在圆心上 D、点在圆上或圆内7. 如图,在Rt△ABC中∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是( )
A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定8. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )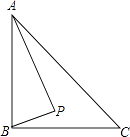 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
9. 点 到 上一点 的距离 的最大值是 , 的最小值为 ,则 的半径为 .10. 在矩形ABCD中,BC=6,CD=8,以A为圆心画圆,且点D在⊙A内,点B在⊙A外,则⊙A半径r的取值范围是 .
 11. △ABC中,∠C=90°,AB=4cm,BC=2cm,以点A为圆心,以3.4cm的长为半径画圆,则点C在⊙O , 点B在⊙O .12. 若一个点到圆心的距离恰好等于半径,则此点必在;若一个点到圆心的距离大于半径,则此点必在;若一个点到圆心的距离小于半径,则此点必在 .13. 在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是 .
11. △ABC中,∠C=90°,AB=4cm,BC=2cm,以点A为圆心,以3.4cm的长为半径画圆,则点C在⊙O , 点B在⊙O .12. 若一个点到圆心的距离恰好等于半径,则此点必在;若一个点到圆心的距离大于半径,则此点必在;若一个点到圆心的距离小于半径,则此点必在 .13. 在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是 . 14. 如图,⊙O的半径为1,P是⊙O外一点,OP=2,Q是⊙O上的动点,线段PQ的中点为M,连接OP、OM,则线段OM的最小值是 .
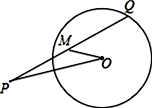
14. 如图,⊙O的半径为1,P是⊙O外一点,OP=2,Q是⊙O上的动点,线段PQ的中点为M,连接OP、OM,则线段OM的最小值是 . 15. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
15. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
三、解答题
-
16. 已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.17. 在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,判断A,B两点和⊙C的位置关系.18. ⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5 cm,问:A、B、C三点与⊙O的位置关系各是怎样?