江苏省扬州市邵樊片2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-04 类型：期中考试

进入出卷网下载

一、单选题

1. 下列一元二次方程中，有实数根的是（）

A、x²－x＋1＝0 B、x²－2x+3＝0 C、x²+x－1＝0 D、x²＋4＝0

查看试题解析
2. 已知⊙O的直径为6cm，点A不在⊙O内，则OA的长（）

A、大于3cm B、不小于3cm C、大于6cm D、不小于6cm

查看试题解析
3. 下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧.其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心.若∠B=25°，∠C的大小等于（）

A、20° B、25° C、40° D、50°

查看试题解析
5. 已知关于x的一元二次方程（m﹣2）x²+3x+m²﹣4=0有一个解为0，则m的值为（）

A、2 B、﹣2 C、±2 D、0

查看试题解析
6. 某校九年级举办传统文化进校园朗诵大赛，小明同学根据比赛中九位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（）
中位数
众数
平均数
方差
9.2
9.3
9.1
0.3

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
7. ⊙O的半径为10，两平行弦AC，BD的长分别为12，16，则两弦间的距离是（）

A、2 B、14 C、6或8 D、2 或14

查看试题解析
8. 如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD对角线的交点，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）

A、4 B、 $\frac{21}{5}$ C、 $\frac{35}{8}$ D、 $\frac{17}{4}$

查看试题解析

二、填空题

9. 请你写出一个有一根为1的一元二次方程：.

查看试题解析
10. 在一个不透明的口袋中，装有若干个颜色不同其余都相同的球．如果口袋中装有3个红球且摸到红球的概率为 $\frac{1}{5}$ ，那么口袋中球的总个数为．

查看试题解析
11. 若直角三角形的两条直角边为5和12，则这个直角三角形的内切圆半径为.

查看试题解析
12. 某家用电器经过两次降价，每台零售价由1800元下降到1458元.若两次降价的百分率相同，设这个百分率为x，则可列出关于x的方程为.

查看试题解析
13. 如果圆锥的母线为4cm，底面半径为3cm，那么这个圆锥的侧面积为．

查看试题解析
14. 如图，四边形ABCD是平行四边形，其中边AD是⊙O的直径，BC与⊙O相切于点B，若⊙O的周长是12π，则四边形ABCD的面积为．

查看试题解析
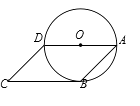15. 若关于x的一元二次方程 $k x^{2} + 2 (k + 1) x + k - 1 = 0$ 有两个不相等的实数根，则k的取值范围是.

查看试题解析
16. 现有一个圆心角为180°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计）．该圆锥底面圆的半径为cm．

查看试题解析
17. 如图，在△ABC中，AB＝6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是.

查看试题解析
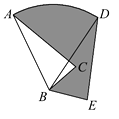18. 如图，在直角坐标系中，已知点A（0，1），点P在线段OA上，以AP为半径的⊙P周长为1．点M从A开始沿⊙P按逆时针方向转动，射线AM交x轴于点N（n，0），设点M转过的路程为m（0＜m＜1）．随着点M的转动，当m从 $\frac{1}{3}$ 变化到 $\frac{2}{3}$ 时，点N相应移动的路径长为．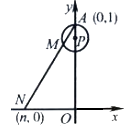

查看试题解析

三、解答题

19. 解下列方程：

(1)、(x－5)²＝x－5

(2)、x²+12x+27=0（配方法）.

查看试题解析
20. 已知：关于x的方程mx²+（m-3）x-3=0（m≠0）．

(1)、求证：方程总有两个实数根；

(2)、如果m为正整数，且方程的两个根均为整数，求m的值．

查看试题解析
21. 九（2）班组织了一次知识竞赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算乙队的平均成绩和方差；

(3)、已知甲队成绩的方差是1.4，则成绩较为整齐的是队.

查看试题解析
22. 商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．

(1)、若他去买一瓶饮料，则他买到奶汁的概率是；

(2)、若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．

查看试题解析
23. 某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高1元，其每天的销售量就减少20件.

(1)、当售价定为12元时，每天可售出件；

(2)、要使每天利润达到640元，则每件售价应定为多少元？

查看试题解析
24. 如图，PA，PB分别与⊙O相切于点A，B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N.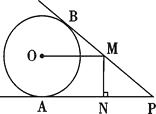

(1)、求证：OM = AN；

(2)、若⊙O的半径R=3，PA=9，求OM的长.

查看试题解析
25. 如图，AC是⊙O的直径，点B，D在⊙O上，点E在⊙O外，∠EAB=∠D=30°．

(1)、∠C的度数为；

(2)、求证：AE是⊙O的切线；

(3)、当AB=3时，求图中阴影部分的面积（结果保留根号和π）．

查看试题解析
26. 阅读新知：化简后，一般形式为ax⁴+bx²+c=0(a≠0)的方程，由于其具有只含有未知数偶次项的四次方程，我们称其为“双二次方程”．这类方程我们一般可以通过换元法求解．如：求解2x⁴-5x²+3=0的解．
解：设 $x^{2} = t$ ，则原方程可化为： $2 t^{2} - 5 t + 3 = 0$ ，解之得 $t_{1} = 1 ， t_{2} = \frac{3}{2}$
当 $t_{1} = 1$ 时， $x^{2} = 1$ ，∴ $x_{1} = 1 ， x_{2} = - 1$ ；
当 $t_{2} = \frac{3}{2}$ 时 $x^{2} = \frac{3}{2}$ ，∴ $x_{3} = \frac{\sqrt{6}}{2} ， x_{4} = - \frac{\sqrt{6}}{2}$ ．
综上，原方程的解为： $x_{1} = 1 ， x_{2} = - 1$ ， $x_{3} = \frac{\sqrt{6}}{2} ， x_{4} = - \frac{\sqrt{6}}{2}$ .

(1)、通过上述阅读，请你求出方程 $3 y^{4} + 8 y^{2} - 3 = 0$ 的解；

(2)、判断双二次方程ax⁴+bx²+c=0(a≠0)根的情况，下列说法正确的是（选出正确的答案)．
①当b²-4ac≥0时，原方程一定有实数根；
②当b²-4ac<0时，原方程一定没有实数根；
③原方程无实数根时，一定有b²-4ac<0．

查看试题解析
27. 已知，在平面直角坐标系中，点P（0，2），以P为圆心，OP为半径的半圆与y轴的另一个交点是C，一次函数 $y = - \frac{\sqrt{3}}{3} x + m$ （m为实数）的图象为直线l，l分别交x轴，y轴于A，B两点，如图1．

(1)、B点坐标是（用含m的代数式表示），∠ABO=°．

(2)、若点N是直线AB与半圆CO的一个公共点（两个公共点时，N为右侧一点），过点N作⊙P的切线交x轴于点E，如图2．是否存在这样的m的值，使得△EBN是直角三角形．若存在，求出m的值；若不存在，请说明理由．

查看试题解析
28. 如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．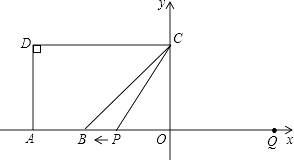

(1)、求点C的坐标；

(2)、当∠BCP=15°时，求t的值；

(3)、以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．

查看试题解析

中位数	众数	平均数	方差
9.2	9.3	9.1	0.3

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9