江苏省如皋市南片区八校联考2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-04 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线y=（x﹣2）²﹣3的顶点坐标是（）

A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）

查看试题解析
2. 已知⊙O的半径为3cm，点P到圆心O的距离OP=2cm，则点P（）

A、在⊙O外 B、在⊙O上 C、在⊙O内 D、在⊙O上或在⊙O内

查看试题解析
3. 关于二次函数 $y = - \frac{1}{2} x^{2}$ 的图象及其性质的说法错误的是（）

A、开口向下 B、顶点是原点 C、对称轴是y轴 D、y随x的增大而减小

查看试题解析
4. 如图，已知AB 、AD是⊙O的弦，∠BOD=50°，则∠BAD的度数是（）

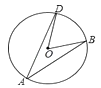A、50° B、40° C、25° D、35°

查看试题解析
5. 已知点（2，﹣4）在反比例函数图象上，则下列各点在此函数图象上的是（）

A、（2，4） B、（﹣1，﹣8） C、（﹣2，﹣4） D、（4，﹣2）

查看试题解析
6. 在Rt△ABC中，∠C=90°，AC=6，BC=8，则这个三角形的外接圆的半径是（）

A、10 B、5 C、4 D、3

查看试题解析
7.
如图，四边形ABCD内接于圆O，E为CD延长线上一点，若∠B=110°，则∠ADE的度数为（　　）

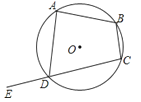A、115° B、110° C、90° D、80°

查看试题解析
8. 若函数 $y = - \frac{a^{2} + 1}{x}$ 的图象上有三个点（﹣1，y₁），（ $- \frac{1}{2}$ ，y₂），（ $\frac{1}{2}$ ，y₃），则y₁ ， y₂ ， y₃必的大小关系是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₂＜y₁＜y₃

查看试题解析
9. 如图，是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度增加（）m．

A、1 B、2 C、 $2 \sqrt{6} - 4$ D、 $\sqrt{6} - 2$

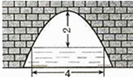查看试题解析
10. 已知，二次函数y=x²﹣2x+a（a是实数），当自变量任取x₁ ， x₂时，分别与之对应的函数值y_l ， y₂满足y₁＞y₂ ，则x₁ ， x₂应满足的关系式是（）

A、x_l﹣1＜x₂﹣1 B、x₁﹣1＞x₂﹣1 C、|x₁﹣l|＜|x₂﹣1| D、|x₁﹣1|＞|x₂﹣1|

查看试题解析

二、填空题

11. 把抛物线 $y = x^{2}$ 向左平移2个单位，则平移后所得抛物线的解析式为．

查看试题解析
12. 若双曲线 $y = \frac{k - 3}{x}$ 的图象在第一、三象限，则k的取值范围是．

查看试题解析
13. 如图，某扇形纸扇完全打开后，外侧两竹条AB，AC的夹角为120°，AB长为27厘米，则 $\overset{⌢}{B C}$ 的长为厘米．（结果保留π）

查看试题解析
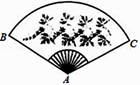14. 已知抛物线y=x²﹣x﹣1与x轴的一个交点为（a，0），则代数式a²﹣a+2018的值为．

查看试题解析
15. 圆锥的底面半径为2，母线长为6，则它的侧面积为．

查看试题解析
16. 如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB=13，AC=5，BC=12，阴影部分是△ABC的内切圆，这个圆的半径为．

查看试题解析
17. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=m．若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为m² ．

查看试题解析
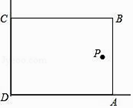18. 如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y=﹣x+6于A、B两点，若反比例函数 $y = \frac{k}{x}$ （x＞0）的图象与△ABC有公共点，则k的取值范围是．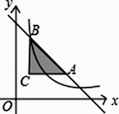

查看试题解析

三、解答题

19. 如图，在⊙O中，弦AB的长为8，圆心O到AB的距离为3．

(1)、求⊙O的半径；

(2)、若点P是AB上的一动点，试直接写出线段OP的取值范围．

查看试题解析
20. 已知二次函数y=x²﹣4x+3．

(1)、用配方法将此二次函数化为y=a（x﹣h）²+k的形式；

(2)、在所给的坐标系上画出这个二次函数的大致图象；

(3)、观察图象填空：当x＜2时，y随x的增大而．

查看试题解析
21. 一辆汽车从甲地开往乙地，随着汽车平均速度v（km/h）的变化，所需时间t（h）的变化情况如图所示．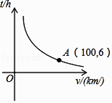

(1)、甲、乙两地相距km；t与v之间的函数关系式是；

(2)、当汽车的平均速度为75km/h时，从甲地到乙地所需时间为多少h？

查看试题解析
22. 已知反比例函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = a x + b$ 的图象交于点A（1，4）和点B（m，﹣2）．

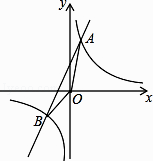(1)、求一次函数的关系式；

(2)、求△AOB的面积；

(3)、观察图象，写出使得y₁≤y₂成立的自变量x的取值范围．

查看试题解析
23. 已知二次函数 $y = x^{2} + 2 (m - 1) x + m^{2} - 1$ 与 $x$ 有轴两个不同的交点．

(1)、求实数 $m$ 的取值范围；

(2)、若两个交点分别为（ $x_{1}$ ，0）、（ $x_{2}$ ，0），问是否存在实数 $m$ ，使得 $x_{1} x_{2} = 0$ 成立？如果存在，求出 $m$ 的值；如果不存在，请说明理由．

查看试题解析
24. 如图

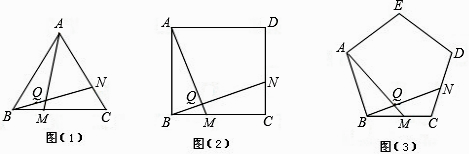(1)、如图（1），已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，BM=CN．求出∠BQM的度数；

(2)、将（1）中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…，“点N是AC上一点”改为点N是CD上一点，其余条件不变，分别推断出∠BQM等于多少度，将结论填入下表：
正多边形
正方形
正五边形
……
正n边形
∠BQM的度数

……

查看试题解析
25. 如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．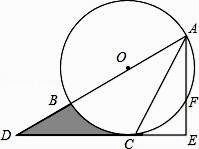

(1)、求证：DE是⊙O的切线；

(2)、若AE=6，∠D=30°，求图中阴影部分的面积．

查看试题解析
26. 某商店将每件进价为80元的某种商店按每件110元出售，每天可售出100件．该商店想通过降低售价、增加销售量的方法来提高利润．经市场调查，发现这种商品每件每降价5元，每天的销售量可增加50件．设商品降价x元，每天销售该商品获得的利润为y元．

(1)、求y（元）关于x（元）的函数关系式，并写出x的取值范围．

(2)、求当x取何值时y最大？并求出y的最大值．

(3)、若要是每天销售利润为3750元，且尽可能最大的向顾客让利，应将该商品降价多少元？

查看试题解析
27. 如图，已知抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．

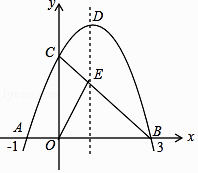(1)、求此抛物线的解析式；

(2)、求点C和点D的坐标；

(3)、若点P在第一象限内的抛物线上，且S_△_ABP=4S_△_COE ，求P点坐标．

查看试题解析
28. 在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点（1，1），（﹣ 2，﹣ 2），（ $\sqrt{2}$ ， $\sqrt{2}$ ），…，都是梦之点，显然梦之点有无数个．

(1)、若点 P（2，b）是反比例函数 $y = \frac{n}{x}$ (n为常数，n≠0)的图象上的梦之点，求这个反比例函数解析式；

(2)、⊙O的半径是 $\sqrt{2}$ ，
①求出⊙O上的所有梦之点的坐标；
②已知点M（m，3），点Q是（1）中反比例函数 $y = \frac{n}{x}$ 图象上异于点P的梦之点，过点Q的直线l与y轴交于点A，∠OAQ＝45°．若在⊙O上存在一点N，使得直线MN∥l或MN⊥l ，求出m的取值范围．

查看试题解析

正多边形	正方形	正五边形	……	正n边形
∠BQM的度数			……