江苏省邗江区2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-04 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 一元二次方程x2+2x＝0的根是（ ）
    A、x1＝0，x2＝－2 B、x1＝1，x2＝2 C、x1＝1，x2＝－2 D、x1＝0，x2＝2

    查看试题解析

  • 2. 如图，AB为⊙O的直径，点C在⊙O上，∠A=40°，则∠B的度数为（   ）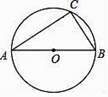


    A、65° B、50° C、130° D、80°

    查看试题解析

  • 3. 用配方法解一元二次方程x2＋3＝4x，下列配方正确的是（   ）
    A、(x＋2)2＝2 B、(x－2)2＝7 C、(x＋2)2＝1 D、(x－2)2＝1

    查看试题解析

  • 4. 若圆的半径是5，圆心的坐标是（0，0），点P的坐标是（-4，3），则点P与⊙O的位置关系是（     ）
    A、点P在⊙O外   B、点P在⊙O内 C、点P在⊙O上  D、点P在⊙O外或⊙O上

    查看试题解析

  • 5. 已知实数x1 ， x2满足x1＋x2＝7，x1x2＝－12，则以x1 ， x2为根的一元二次方程是（ ）
    A、x2－7x＋12＝0 B、x2－7x－12＝0 C、x2＋7x－12＝0 D、x2＋7x＋12＝0

    查看试题解析

  • 6. 下列命题中，真命题的个数是（   ）

    ①经过三点一定可以作圆；②平分弦的直径必定垂直于这条弦；③在同圆或等圆中，相等的圆心角所对的弧相等；④三角形的外心到三角形三边的距离相等．

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 7. 若 a−b+c=0 ，则关于x的一元二次方程 ax2+bx+c=0(a≠0) 必有一根为（   ）
    A、1 B、0 C、−1 D、−1 或 1

    查看试题解析

  • 8. 在半径为R的圆内，长为R的弦所对的圆周角为（   ）
    A、30° B、60° C、30°或150° D、120°或60°

    查看试题解析

二、填空题

  • 9. 把方程3x（x﹣2）=4（x+1）化为一元二次方程的一般形式是；

    查看试题解析

  • 10. 某种衬衣的价格经过连续两次降价后，由每件100元降至64元，设平均每次降价的百分率为x，则可列方程为.

    查看试题解析

  • 11. 如图，⊙O是△ABC的外接圆，∠OCB=30°，则∠A的度数等于 ．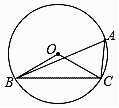

    查看试题解析

  • 12. 已知正六边形的周长为30，那么正六边形的半径为 ．

    查看试题解析

  • 13. 写出一个以1和-2为两根的一元二次方程（二次项系数为1） ．

    查看试题解析

  • 14. 若圆锥的底面直径为6 cm，母线长为5 cm，则它的侧面积为.(结果保留π)

    查看试题解析

  • 15. 三角形两边的长是3和4，第三边的长是方程x2﹣12x+35=0的根，则该三角形的周长为 ．

    查看试题解析

  • 16. 如图，⊙O的半径为5cm，弦AB为8cm，P为弦AB上的一动点，若OP的长度为整数，则满足条件的点P有个．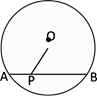

    查看试题解析

  • 17. 若关于x的方程kx2-2x-1=0有两个实数根，则实数k的取值范围是.

    查看试题解析

  • 18. 如图，将弧BC沿弦BC折叠交直径AB于点D，若AD=2，DB=3，则BC的长是 ．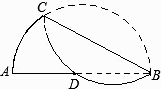

    查看试题解析

三、解答题

  • 19. 解下列方程：     
    (1)、（x﹣2）2=3（x﹣2）
    (2)、x2+3x﹣2=0．

    查看试题解析

  • 20. 如图： AC⌢=BC⌢ ，D、E分别是半径OA和OB的中点，求证：CD=CE．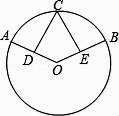

    查看试题解析

  • 21. 定义一种新的运算方式： Cn2=n(n−1)2 （其中 n≥2 ， 且n是正整数 ），例如 C32=3(3−1)2=3 ， C52=5(5−1)2=10 .
    (1)、计算 C102 ；
    (2)、若 Cn2=36 ，求 n ；

    查看试题解析

  • 22. 如图，在四边形ABCD中，∠A=∠C=90°．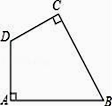

    (1)、用直尺和圆规作⊙O，使它经过A、B、D三点（保留作图痕迹）；
    (2)、点C是否在⊙O上？请说明理由．

    查看试题解析

  • 23. 已知，关于x的方程x2﹣2mx+m2﹣1=0
    (1)、不解方程，判别方程的根的情况；
    (2)、若x=2是方程的一个根，请求出m的值以及它的另一个根．

    查看试题解析

  • 24. 如图，△ABC的三边分别切⊙O于D，E，F．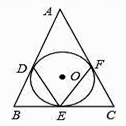

    (1)、若∠A=40°，求∠DEF的度数；
    (2)、AB=AC=13，BC=10，求⊙O的半径．

    查看试题解析

  • 25. 水果店张阿姨以每斤2元的利润出售一种水果，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.2元，每天可多售出40斤，为保证每天至少售出260斤，张阿姨决定降价销售．
    (1)、若将这种水果每斤的售价降低x元，则每天的销售量是斤(用含x的代数式表示)；
    (2)、销售这种水果要想每天赢利300元，张阿姨需将这种水果每斤的售价降低多少元？

    查看试题解析

  • 26. 如图，已知⊙O是△ABC的外接圆，AC是直径，∠A=30°，BC=4，点D是AB的中点，连接DO并延长交⊙O于点P．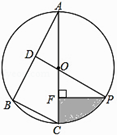

    (1)、求劣弧PC的长（结果保留π）；
    (2)、过点P作PF⊥AC于点F，求阴影部分的面积（结果保留π）．

    查看试题解析

  • 27. △ABC中，∠B=90°，AB=9，BC=12，点p从点A开始延边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P．Q分别从A．B同时出发，当点Q运动到点C时，两点停止运动，问：


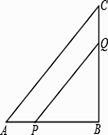    (1)、填空：BQ= ， PB=（用含t的代数式表示）
    (2)、经过几秒，PQ的长为 62 cm？
    (3)、经过几秒， ΔPBQ 的面积等于 8cm2 ?

    查看试题解析

  • 28. 如图，在平面直角坐标系中，⊙P经过x轴上一点C，与y轴分别相交于A、B两点，连接AP并延长分别交⊙P、x轴于点D、点E，连接DC并延长交y轴于点F，且DC=FC，点D的坐标为（12，－2）．

    (1)、判断⊙P与x轴的位置关系，并说明理由；
    (2)、求⊙P半径；
    (3)、若弧BD上有一动点M，连接AM，过B点作BN⊥AM，垂足为N，连DN，则DN的最小值是 ．

    查看试题解析