江苏省东台市2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-04 类型:期中考试
一、单选题
-
1. a,b,c是常数,下列方程中是关于x的一元二次方程的是( )A、x2+ =3 B、x2﹣y2=0 C、x2+x﹣2=0 D、ax2+bx+c=02. 下列函数解析式中,一定为二次函数的是( )A、y=x+3 B、y=ax2+bx+c C、y=t2﹣2t+2 D、y=x2+3. 一列数4,5,6,4,4,7,x的平均数是5,则x的值为( )A、4 B、5 C、6 D、74. 袋中装有1个绿球,2个黑球和3个红球,它们除颜色外其余均相同,从袋中摸出一个球,则摸出黑球的概率是( )A、 B、 C、 D、5. 如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为( )
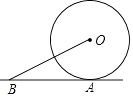 A、1 B、2 C、 D、26. 用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的圆心角度数是( )
A、1 B、2 C、 D、26. 用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的圆心角度数是( )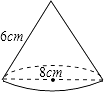 A、150° B、180° C、200° D、240°7. 将函数y=kx2与y=kx+k的图象画在同一个直角坐标系中,可能的是( )A、
A、150° B、180° C、200° D、240°7. 将函数y=kx2与y=kx+k的图象画在同一个直角坐标系中,可能的是( )A、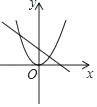 B、
B、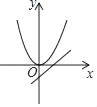 C、
C、 D、
D、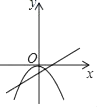 8. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )
8. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 请写一个两根分别是﹣3和2的一元二次方程 .10. 某学习小组全体同学都为本组其他人员送了一张新年贺卡,若全组共送贺卡78张,设这个小组的同学共有x人,可列方程: .11. 拋物线的顶点为(2,﹣3),与y轴交于点(0,﹣7),则该抛物线的解析式为 .12. 若圆锥的底面半径为3cm,高为4cm,则它的侧面展开图的面积为cm2 .13. 为了比较甲、乙两种水稻秧苗哪种出苗更整齐,各随机抽取50株,量出每株长度,发现两组秧苗的平均长度一样,甲、乙的方差分别是3.5,10.9,则出苗更整齐的是(填“甲”或“乙”).14. 在进行某批乒乓球的质量检验时,当抽取了2000个乒乓球时,发现优等品有1898个,则这批乒乓球“优等品”的概率的估计值是(精确到0.01).
15. 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=100°,则∠DCE的大小是 .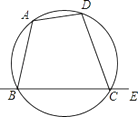 16. 将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= .17. 如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是°.
16. 将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= .17. 如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是°.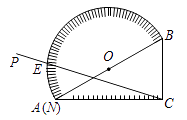 18. 对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y = ax2+ bx + c(a≠0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是.
18. 对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y = ax2+ bx + c(a≠0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是.三、解答题
-
19. 解一元二次方程(1)、2(x﹣3)2﹣18=0(2)、x2﹣5x+3=020. 某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛其预赛成绩如图:
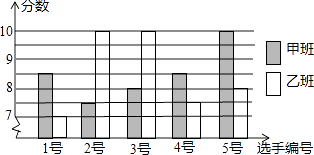 (1)、根据上图填写下表
(1)、根据上图填写下表平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6
(2)、根据上表中的平均数和中位数你认为哪班的成绩较好?并说明你的理由21. 小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A、空调车B、普通车a,换乘站点可选择空调车C,普通车b、普通车c,且均在同一站点换乘.空调车投币2元,普通车投币1元.(1)、求小明在出发站点乘坐空调车的概率;(2)、求小明到达植物园恰好花费3元公交费的概率.22. 设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.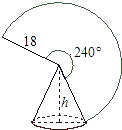 23. 已知二次函数 的图像经过点(2, ).(1)、求这个二次函数的函数解析式;(2)、若抛物线交x轴于A,B两点,交y轴于C点,顶点为D,求以A、B、C、D为顶点的四边形面积.24. 如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
23. 已知二次函数 的图像经过点(2, ).(1)、求这个二次函数的函数解析式;(2)、若抛物线交x轴于A,B两点,交y轴于C点,顶点为D,求以A、B、C、D为顶点的四边形面积.24. 如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).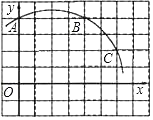 (1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;(2)、点M的坐标为;(3)、判断点D(5,﹣2)与⊙M的位置关系.25. 如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;(2)、点M的坐标为;(3)、判断点D(5,﹣2)与⊙M的位置关系.25. 如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.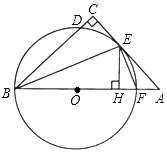 (1)、求证:AC是⊙O的切线;(2)、过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)、求证:CD=HF.26. 如图,抛物线y=﹣ + +2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.
(1)、求证:AC是⊙O的切线;(2)、过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)、求证:CD=HF.26. 如图,抛物线y=﹣ + +2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.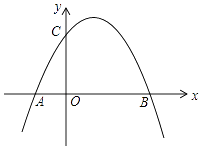 (1)、求A,B两点坐标.(2)、连结AC,若点P在第一象限的抛物线上,P的横坐标为t,四边形ABPC的面积为S.试用含t的式子表示S,并求t为何值时,S最大.(3)、在(2)的基础上,在整条抛物线上和对称轴上是否分别存在点G和点H,使以A,G,H,P四点构成的四边形为平行四边形?若存在,请直接写出G,H的坐标;若不存在,请说明理由.27. 平面直角坐标系xOy中,过原点O及点A(0,4)、C(12,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒2 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒4个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
(1)、求A,B两点坐标.(2)、连结AC,若点P在第一象限的抛物线上,P的横坐标为t,四边形ABPC的面积为S.试用含t的式子表示S,并求t为何值时,S最大.(3)、在(2)的基础上,在整条抛物线上和对称轴上是否分别存在点G和点H,使以A,G,H,P四点构成的四边形为平行四边形?若存在,请直接写出G,H的坐标;若不存在,请说明理由.27. 平面直角坐标系xOy中,过原点O及点A(0,4)、C(12,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒2 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒4个单位长度的速度沿x轴正方向移动.设移动时间为t秒. (1)、当点P移动到点D时,求出此时t的值.(2)、当t为何值时,△PQB为直角三角形.(3)、已知过O、P、Q三点的抛物线解析式为y=﹣ .问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当点P移动到点D时,求出此时t的值.(2)、当t为何值时,△PQB为直角三角形.(3)、已知过O、P、Q三点的抛物线解析式为y=﹣ .问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.