湖北省武昌区C组联盟2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-04 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程3x²﹣x﹣2=0的二次项系数、一次项系数、常数项分别是（）

A、3，﹣1，﹣2 B、3，1，﹣2 C、3，﹣1，2 D、3，1，2

查看试题解析
2. 二次函数 $y = 2 {(x - 1)}^{2} + 3$ 的图象的顶点坐标是（）

A、 $(- 2 ， 3)$ B、 $(2 ， 3)$ C、 $(1 ， - 3)$ D、 $(1 ， 3)$

查看试题解析
3. 下列四个黑体字母中，既是轴对称图形，又是中心对称图形的是（）

A、C B、L C、X D、Z

查看试题解析
4. 在平面直角坐标系中，点 $P (- 3 ， 2)$ 关于原点对称点 $P^{'}$ 的坐标为（）

A、 $(3 ， 2)$ B、 $(2 ， - 3)$ C、 $(- 3 ， - 2)$ D、 $(3 ， - 2)$

查看试题解析
5. 解一元二次方程x²-4x+1=0，用配方法可变形为（）

A、 ${(x - 2)}^{2} = - 1$ B、 ${(x - 4)}^{2} = 5$ C、 ${(x - 2)}^{2} = 5$ D、 ${(x - 2)}^{2} = 3$

查看试题解析
6. 关于 $x$ 的一元二次方程 $x^{2} - x - 2 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根

查看试题解析
7. 抛物线y=x²上有三个点（1，y₁），（－2，y₂），（3，y₃），那么，y₁、y₂、y₃的大小关系是（）

A、y₁<y₂<y₃ B、y₃<y₂<y₁ C、y₁<y₃<y₂ D、y₂<y₃<y₁

查看试题解析
8. 某旅游景点参观人数逐年增加，据有关部门统计， $2$ 016年约为 $20$ 万人次， $2$ 018年约为 $2$ 8.8万人次，设观赏人数年均增长率为 $x$ ，则下列方程中正确的是（）

A、 $20 (1 + 2 x) = 28.8$ B、 $28.8 {(1 + x)}^{2} = 20$ C、 $20 {(1 + x)}^{2} = 28.8$ D、 $20 + 20 (1 + x) + 20 {(1 + x)}^{2} = 28.8$

查看试题解析
9. 在平面直角坐标系中，抛物线y=－ $\frac{1}{2}$ x²+2x－1关于点（－1，2）对称的图象解析式为（）

A、y= $\frac{1}{2}$ x²－2x+1 B、y= $\frac{1}{2}$ x²+4x+11 C、y=－ $\frac{1}{2}$ x²－2x-1 D、y= $\frac{1}{2}$ x²+4x+19

查看试题解析
10. 当 $- 2 \leq x \leq 1$ 时，二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ 有最大值 $4$ ，则实数 $m$ 的值为（）

A、 $- \frac{7}{4}$ B、 $\sqrt{3} 或 - \sqrt{3}$ C、 $2 或 - \sqrt{3}$ D、2或 $\sqrt{3}$ 或 $- \frac{7}{4}$

查看试题解析

二、填空题

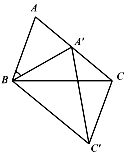
11. 若 $x = 2$ 是一元二次方程x²+ $a$ =0的解，则 $a$ 的值为。

查看试题解析
12. 把函数 $y = - 2 x^{2}$ 的图象向上平移 $2$ 个单位，所得的抛物线的函数关系式为。

查看试题解析
13. 某学校九年级组织了一次乒乓球比赛，每班派一名同学代表班级进行比赛，参赛的每两个队之间都要比赛一场，共比赛 $28$ 场，该校九年级共有个班级。

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A = 70^{\circ}$ ， $A C = B C$ ，以点 $B$ 为旋转中心把 $△ A B C$ 按顺时针旋转 $α$ 度，得到 $△ A^{'} B C^{'}$ ，点 $A$ '恰好落在 $A C$ 上，连接CC′，则∠ACC'= ．

查看试题解析
15. 若函数 $y = (a - 1) x^{2} - 4 x + 2 a$ 的图象与 $x$ 轴有且只有一个交点，则 $a$ 的值为。

查看试题解析
16. 如图，四边形 $A B C D$ 是菱形， $A$ B=6，且∠ABC=60°，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为。

查看试题解析

三、解答题

17. 解方程：x²＋3x－1=0

查看试题解析
18. 如图， $△ A B C$ 和 $△ D E F$ 关于点 $O$ 成中心对称.

(1)、作出它们的对称中心 $O$ ，并简要说明作法；

(2)、若 $A B = 6$ ， $A C = 5$ ， $B C = 4$ ，求 $△ D E F$ 的周长；

(3)、连接 $A F$ ， $C D$ ，试判断四边形 $A C D F$ 的形状，并说明理由．

查看试题解析
19. 有一条长40cm的绳子，要把它围成一个矩形，若设矩形的一边长为xcm，回答以下问题：

(1)、怎样围成一个面积为75cm²的矩形？

(2)、能围成一个面积为101cm²的矩形吗？如能，说明围法；如不能，说明理由。

查看试题解析
20. 如图，在平面直角坐标系中，在边长为 $1$ 个单位长度的小正方形组成的方格中，点 $A ， B ， C$ 都在格点上．

(1)、画出ΔABC绕着点B逆时针旋转90°得到的ΔA'B'C'，并写出的A'的坐标

(2)、在（1）的情况下，直接写出线段AA’的长度．

(3)、在y轴上找一点P，使ΔPAB的周长最小，直接写出P的坐标．

查看试题解析
21. 某超市销售一种饮料，平均每天可售出100箱，每箱利润120元．为了扩大销售，增加利润，超市准备适当降价．据测算，若每箱降价1元，每天可多售出2箱．

(1)、如果要使每天销售饮料获利14000元，问每箱应降价多少元？

(2)、每箱降价多少元超市每天获利最大？最大利润是多少？

查看试题解析
22. 如图，是一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是 $1 m$ ，拱桥的跨度为 $10 m$ ，桥洞与水面的最大距离是 $5 m$ ，桥洞两侧壁上各有一盏距离水面 $4 m$ 的景观灯，把拱桥的截面图放在平面直角坐标系中。

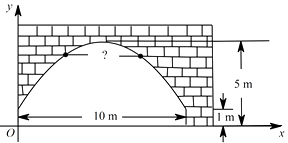(1)、求抛物线对应的函数解析式，并写出自变量的取值范围；

(2)、求两盏景观灯之间的水平距离。

查看试题解析
23. 已知：正方形 $A B C D$ 中， $∠ M A N = 45^{\circ}$ ， $∠ M A N$ 绕点 $A$ 顺时针旋转，它的两边分别交 $C B$ ， $D C$ （或它们的延长线）于点 $M$ ， $N$ 。当 $∠ M A N$ 绕点 $A$ 旋转到 $B M = D N$ 时（如图1），易证 $M N = B M + D N$ ．（不必证明）

(1)、当 $∠ M A N$ 绕点 $A$ 旋转到 $B M \neq D N$ 时（如图2），线段 $B M$ ， $D N$ 和 $M N$ 之间有怎样的数量关系？写出猜想，并加以证明。

(2)、当 $∠ M A N$ 绕点 $A$ 旋转到如图3的位置时，线段 $B M$ ， $D N$ 和 $M N$ 之间又有怎样的数量关系？写出猜想，并加以证明。

查看试题解析
24. 如图，抛物线y=ax²+bx-3与 $x$ 轴交于 $A$ ， $B$ 两点（ $A$ 点在 $B$ 点左侧），A(-1，0)，B(3，0)，直线 $l$ 与抛物线交于 $A$ ， $C$ 两点，其中 $C$ 点的横坐标为 $2$ 。

(1)、求抛物线的函数解析式；

(2)、 $P$ 是线段 $A C$ 上的一个动点，过 $P$ 点作 $y$ 轴的平行线交抛物线于 $E$ 点，求线段 $P E$ 长度的最大值；

(3)、点 $G$ 是抛物线上的动点，在 $x$ 轴上是否存在点 $F$ ，使 $A$ ， $C$ ， $F$ ， $G$ 这样的四个点为顶点的四边形是平行四边形?如果存在，求出所有满足条件的 $F$ 点坐标；如果不存在，请说明理由。

查看试题解析