湖北省沙洋县2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-04 类型:期中考试
一、单选题
-
1. 一元二次方程3x2=5x+2的二次项的系数为3,则一次项的系数和常数项分别为( )A、5,2 B、5,﹣2 C、﹣5,2 D、﹣5,﹣22. 下列学生喜欢的手机应用软件图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用配方法解一元二次方程x2﹣6x+8=0时,则方程变形正确的是( )A、(x﹣3)2=17 B、(x+3)2=17 C、(x﹣3)2=1 D、(x+3)2=14. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x , 可列方程为( )A、 B、 C、 D、5. 抛物线y=﹣ x2向左平移1个单位长度得到抛物线的解析式为( )A、y=﹣ (x+1)2 B、y=﹣ (x﹣1)2 C、y=﹣ x2+1 D、y=﹣ x2﹣16. 二次函数 与一次函数 的图象如图所示,则满 的x的取值范围是( )
3. 用配方法解一元二次方程x2﹣6x+8=0时,则方程变形正确的是( )A、(x﹣3)2=17 B、(x+3)2=17 C、(x﹣3)2=1 D、(x+3)2=14. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x , 可列方程为( )A、 B、 C、 D、5. 抛物线y=﹣ x2向左平移1个单位长度得到抛物线的解析式为( )A、y=﹣ (x+1)2 B、y=﹣ (x﹣1)2 C、y=﹣ x2+1 D、y=﹣ x2﹣16. 二次函数 与一次函数 的图象如图所示,则满 的x的取值范围是( ) A、 B、 或 C、 或 D、7. 二次函数y=2x2﹣1的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )A、抛物线开口向下 B、抛物线的对称轴是直线x=1 C、抛物线经过点(2,1) D、抛物线与x轴有两个交点8. 在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是( )
A、 B、 或 C、 或 D、7. 二次函数y=2x2﹣1的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )A、抛物线开口向下 B、抛物线的对称轴是直线x=1 C、抛物线经过点(2,1) D、抛物线与x轴有两个交点8. 在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是( ) A、7° B、21° C、23° D、34°9. 若 为二次函数y=-x2-4x+5的图象上的三点,则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y310. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、
A、7° B、21° C、23° D、34°9. 若 为二次函数y=-x2-4x+5的图象上的三点,则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y310. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、 B、
B、 C、
C、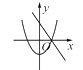 D、
D、 11. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )
11. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )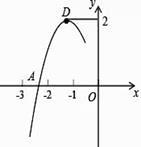 A、1个 B、2个 C、3个 D、4个12. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+ …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
A、1个 B、2个 C、3个 D、4个12. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+ …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )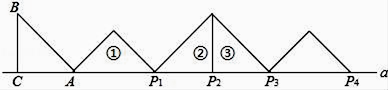 A、1345+376 B、2017+ C、2018+ D、1345+673
A、1345+376 B、2017+ C、2018+ D、1345+673二、填空题
-
13. 点P(﹣3,5)关于原点对称的点的坐标是 .14. 一元二次方程x2+3x=0的解是 .15. 如图,在平面直角坐标系 中,点 A,点 A的坐标分别为(0,2),(-1,0),将线段AB 绕点 O顺时针旋转,若点 A 的对应点A' 的坐标为吗(2,0),则点 B 的对应点B'的坐标为.
 16. 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m,设AD的长为xm,菜园ABCD的面积为ym2 , 则函数y关于自变量x的函数关系式是 , x的取值范围是 .
16. 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m,设AD的长为xm,菜园ABCD的面积为ym2 , 则函数y关于自变量x的函数关系式是 , x的取值范围是 . 17. 已知二次函数y=x2﹣2mx(m为常数),当﹣2≤x≤1时,函数值y的最小值为﹣2,则m的值为 .
17. 已知二次函数y=x2﹣2mx(m为常数),当﹣2≤x≤1时,函数值y的最小值为﹣2,则m的值为 .三、解答题
-
18. 解方程:(1)、 .(2)、(x+3)2=(1﹣2x)2 .19. 已知关于x的方程x2﹣2(m+1)x+m2+2=0.(1)、若方程总有两个实数根,求m的取值范围;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=8,求m的值.20. 如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180º得到ΔFEC。
 (1)、试猜想AE与BF有何关系,并说明理由;(2)、若ΔABC的面积为3cm2 , 求四边形ABFE的面积;(3)、当∠ACB为多少度时,四边形ABFE为矩形?说明理由。21. 如图,直线y=kx+ 与抛物线y= 交于点A(﹣2,0)与点D,直线y=kx+ 与y轴交于点C.
(1)、试猜想AE与BF有何关系,并说明理由;(2)、若ΔABC的面积为3cm2 , 求四边形ABFE的面积;(3)、当∠ACB为多少度时,四边形ABFE为矩形?说明理由。21. 如图,直线y=kx+ 与抛物线y= 交于点A(﹣2,0)与点D,直线y=kx+ 与y轴交于点C. (1)、求k、b的值及点D的坐标;(2)、过D点作DE⊥y轴于点E,点P是抛物线上A、D间的一个动点,过P点作PM∥CE交线段AD于M点,问是否存在P点使得四边形PMEC为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.22. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?23. 如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,
(1)、求k、b的值及点D的坐标;(2)、过D点作DE⊥y轴于点E,点P是抛物线上A、D间的一个动点,过P点作PM∥CE交线段AD于M点,问是否存在P点使得四边形PMEC为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.22. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?23. 如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,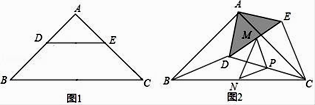 (1)、求证:∠B=∠C,AD=AE;(2)、若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN. ①判断△PMN的形状,并说明理由;②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为 。24. 如图,抛物线y=ax2+bx经过点A(﹣1, )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)、求证:∠B=∠C,AD=AE;(2)、若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN. ①判断△PMN的形状,并说明理由;②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为 。24. 如图,抛物线y=ax2+bx经过点A(﹣1, )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B. (1)、求抛物线的解析式;(2)、如图1,连接AO、BO,若△OAB的面积为5,求m的值;(3)、如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.
(1)、求抛物线的解析式;(2)、如图1,连接AO、BO,若△OAB的面积为5,求m的值;(3)、如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.