江苏省无锡市锡北片2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-12-04 类型：期中考试
一、单选题
-
1. 下列图形中，是轴对称图形的个数是（ ）
A、1个 B、2个 C、3个 D、4个2. 下列几组数中不能作为直角三角形三边长度的是（ ）
A、 B、 C、 D、3. 等腰三角形的一个角是50°，则它的底角是（ ）A、50° B、65° C、80° D、50° 或65°4. 如图，在下列条件中，不能证明△ABD≌△ACD的是（ ）
A、BD＝DC，AB＝AC B、∠B＝∠C，BD＝DC C、∠B＝∠C，∠BAD＝∠CAD D、∠ADB＝∠ADC，BD＝DC5. 如图．射线OC平分∠AOB，点P在OC上，且PM⊥OA于M．PN⊥OB于N，当PM＝2cm时，则PN是（ ）
A、1cm B、2cm C、4cm D、不确定6. 如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）
A、80° B、70° C、60° D、50°7. △ABC中，①若AB＝BC＝CA，则△ABC是等边三角形；②属于轴对称图形，且有一个角为60°的三角形是等边三角形；③有三条对称轴的三角形是等边三角形；④有两个角是60°的三角形是等边三角形，上述结论中正确的有（ ）
A、1个 B、2个 C、3个 D、4个8. 将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E，D分别落在E′、D′，已知∠AFC=76°，则∠CFD′等于（ ）
A、31° B、24° C、28° D、22°9. 如图，在等边三角形ABC中，BC边上的中线AD=6，E是AD上的一个动点，F是边AB上的一个动点，在点E，F运动的过程中，EB+EF的最小值是（ ）
A、5 B、6 C、7 D、810. 如图，直线l1、l2相交于点A，点B是直线外一点，在直线l1、l2上找一点C，使△ABC为一个等腰三角形．满足条件的点C有（ ）
A、2个 B、4个 C、6个 D、8个二、填空题
-
11. 若直角三角形的两条直角边长分别为6和8，则斜边长为 ．
12. 已知ΔABC≌ΔDEF，点A与点D．点B与点E分别是对应顶点，
(1)、若ΔABC的周长为32，AB=10，BC=14，则DF=(2)、∠A=48°，∠B=53°，则∠F=。13. 已知等腰三角形的两条边长分别为3和7，那么它的周长等于 ．14. 如图，等边△ABC中，AD是中线，AD=AE，则∠EDC= ．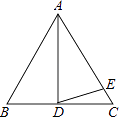
15. 如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=10°，则∠C等于°．
16. 等腰三角形一腰上的高与另一腰的夹角是28°，则顶角是 ．
17. 如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，则四边形ABCD的面积为 ．
三、解答题
-
18. 如图，已知点B、F、C、E在一条直线上，BF＝CE，AB＝DE，∠B＝∠E．求证：AC∥FD．
19. 已知等腰三角形的三边长a＝5x－1，b＝6－x，c＝4，求x的值．
20. 小王剪了两张直角三角形纸片，进行了如下的操作：
(1)、操作一：如图1，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE．
①如果AC＝6cm，BC＝8cm，可求得△ACD的周长为；
②如果∠CAD：∠BAD=4：7，求∠B的度数为；
(2)、操作二：如图2，小王拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，若AC＝9cm，BC＝12cm，请求出CD的长．21. 画图或计算：
(1)、如图1，地面上有三个洞口A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A、B、C三个点的距离相等），尽快抓到老鼠，应该蹲守在何处？请在图2中，用尺规作出猫所蹲守的位置点P．（不写作法，保留作图痕迹）.
(2)、如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
①在图中画出与△ABC关于直线l成轴对称的△AB′C′；
②线段CC′被直线l；
③在直线l上找一点P，使PB+PC的长最短．
22. 如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．
(1)、求证：△AEC≌△BED；
(2)、若∠1=40°，求∠BDE的度数．23. 如图，△ABC中，CF⊥AB，垂足为F，M为BC的中点，E为AC上一点，且ME=MF.
(1)、求证：BE⊥AC；(2)、若∠A＝50°，求∠FME的度数．
24. 一节数学课后，老师布置了一道课后练习题：如图1，已知在Rt△ABC中，AB=BC，∠ABC=90°，O为AC中点．
(1)、如图1，若把三角板的直角顶点放置于点O，两直角边分别与AB、BC交于点M、N，求证：BM=CN；
(2)、若点P是线段AC上一动点，在射线BC上找一点D，使PD=PB，再过点D作BO的平行线，交直线AC于一点E，试在备用图上探索线段ED和OP的关系，并说明理由．并说明理由．
25. 已知△ABC中，AC=6cm，BC=8cm，AB=10cm，CD为AB边上的高．动点P从点A出发，沿着△ABC的三条边逆时针走一圈回到A点，速度为2cm/s，设运动时间为ts.
(1)、求CD的长；(2)、t为何值时，△ACP为等腰三角形？(3)、若M为BC上一动点，N为AB上一动点，是否存在M，N使得AM+MN的值最小，如果有请尺规作出图形（不必求最小值），如果没有请说明理由．