人教版九年级数学上册 24.1.2 垂直于弦的直径（一） 同步练习
试卷更新日期：2018-12-04 类型：同步测试
一、选择题
-
1. 如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为E，如果CE=2，那么AB的长是（ ）
A、4 B、8 C、6 D、102. 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（ ）
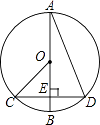A、AD=2OB B、CE=EO C、∠OCE=40° D、∠BOC=2∠BAD3. 如图将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为（ ）
A、2cm B、 cm C、2 cm D、2 cm4.如图，AB是⊙O的弦，OD⊥AB于D，若AO=10 ， OD=6，则AB的长为（ ）
A、8 B、16 C、18 D、205. 如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（ ）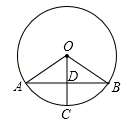
A、2 B、3 C、4 D、56.如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的直径为（ ）
A、5cm B、10cm C、6cm D、14cm7. 如图，⊙O的半径OA=6，以A为圆心，OA为半径的弧交⊙O于B、C点，则BC=（ ）
A、 B、 C、 D、8. ⊙O过点B，C，圆心O在等腰直角△ABC内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（ ）A、 B、2 C、 D、3二、填空题
-
9. 如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为cm．
10. 如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD=1，则弦AB的长是 ．
11. 如图，已知直线AB与⊙O相交于A．B两点，∠OAB=30°，半径OA=2，那么弦AB= ．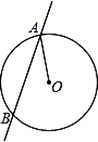
12. 如图所示，已知⊙ 的半径为5，点O到弦AB的距离为3，则⊙ 上到弦 所在直线的距离为2的点有个.
13. 如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为。
14. 如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面积是 ．
15. 如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C、D两点．若∠CMA=45°，则弦CD的长为 ．
三、解答题
-
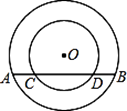
16. 已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．
求证：AC=BD.
17. 已知，如图，M是弧AB的中点，过点M的弦MN交于点C，设圆O的半径为4cm，MN=cm.
(1)、求圆心O到弦MN的距离；(2)、求∠ACM的度数。18. 如图，在⊙O中，CD为直径，AB为弦，且CD平分AB于E，OE=3cm，AB=8cm．求：⊙O的半径．
