2018-2019学年数学北师大版九年级上册6.3反比例函数的应用 同步练习
试卷更新日期：2018-12-04 类型：同步测试
一、选择题
-
1. 如果矩形的面积为6cm2 ， 那么它的长ycm与宽xcm之间的函数图象大致为（ ）A、
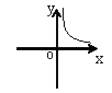B、
C、
D、
2. 三角形的面积为8cm2 ， 这时底边上的高y（cm）与底边x（cm）之间的函数关系用图象来表示是（ ）A、
B、
C、
D、
3. 如图，A，B，C为反比例函数图象上的三个点，分别从A，B，C向x、y轴作垂线，构成三个矩形，它们的面积分别是S1、S2、S3 ， 则S1、S2、S3的大小关系是（ ）
A、S1＝S2＞S3 B、S1＜S2＜S3 C、S1＞S2＞S3 D、S1＝S2＝S34. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数，其图象如图所示．当气球内气压大于120kPa时，气球将爆炸．为了安全起见，气球的体积应（ ）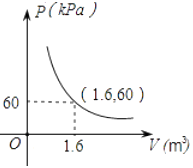
A、不小于 m3 B、小于 m3 C、不小于 m3 D、小于 m3二、填空题
-
5. 如图，根据图中提供的信息，可以写出正比例函数的关系式是；反比例函数关系式是.
6. 已知y与2x成反比例，且当x=3时，y=3，那么当x=3时，y= ， 当y=9时，x=.
7. 长方形的面积为60cm2 ， 如果它的长是ycm，宽是xcm，那么y是x的函数关系，y写成x的关系式是.8. A、B两地之间的高速公路长为300km，一辆小汽车从A地去B地，假设在途中是匀速直线运动，速度为vkm/h，到达时所用的时间是th，那么t是v的函数，t可以写成v的函数关系式是.三、解答题
-
9. 面积一定的梯形，其上底长是下底长的 ，设下底长 时，高 ；(1)、求y与x的函数关系式；
(2)、求当y=5 时，下底长多少？10. 为了预防流感，某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，如图所示.根据图中提供的信息，解答下列问题：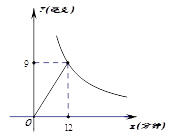
(1)、写出从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；
(2)、据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？
11. 如图所示是某一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)、请你根据图象提供的信息求出此蓄水池的蓄水量；(2)、写出此函数的解析式；
(3)、若要6h排完水池中的水，那么每小时的排水量应该是多少？(4)、如果每小时排水量是5m3 ， 那么水池中的水将要多长时间排完？12. 在研究气体压强和体积关系的物理实验中，一个气球内充满了一定质量的气体，实验中气体温度保持不变，实验人员记录了实验过程中气球内的气体压强p（kPa）与气体体积V（m3）的数据如下表：V（m3）
0.8
1.2
1.6
2.0
2.4
p（kPa）
120
80
60
48
40
(1)、根据表中的数据判断p是V的 ． （①一次函数；②反比例函数；③二次函数．填序号即可）
(2)、确定p与V的函数关系式；
(3)、当气球内的气体压强大于140kPa时，气球将爆炸，为了安全起见，气体的体积V（m3）的取值范围是 ．13. 如图正比例函数y=k1x与反比例函数 交于点A，从A向x轴、y轴分别作垂线，所构成的正方形的面积为4.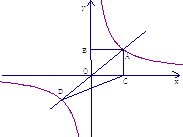
(1)、分别求出正比例函数与反比例函数的解析式；
(2)、求出正、反比例函数图象的另外一个交点坐标。
(3)、求△ODC的面积.