浙江省宁波市七校2016-2017学年八年级3月联考数学试卷

试卷更新日期：2017-03-27 类型：月考试卷

进入出卷网下载

一、选择题

1. 若 $\frac{1}{\sqrt{2 x - 1}}$ 在实数范围内有意义，则 $x \geq 0$ 的取值范围是（）

A、 $x \geq 0$ B、 $x \geq \frac{1}{2}$ C、 $x \neq \frac{1}{2}$ D、 $x > \frac{1}{2}$

查看试题解析
2. 一元二次方程 $3 x^{2} - 3 x = x + 2$ 化为一般形式 $a x^{2} + b x + c = 0$ 后， $a, b, c$ 的值分别是（）

A、3、－3、2 B、3、－4、－2 C、3、－2、2 D、3、－4、2

查看试题解析
3. 方程 $\sqrt{x + 1} = 5 - x$ 的解是（）

A、 $x = 3$ B、 $x = 8$ C、 $x_{1} = 3$ ， $x_{2} = 8$ D、 $x_{1} = 3$ ， $x_{2} = - 8$

查看试题解析
4. 下列一元二次方程有两个相等的实数根的是（）

A、 $x^{2} + 1 = 0$ B、 $x^{2} + 4 x - 4 = 0$ C、 $x^{2} - 2 x + \frac{1}{2} = 0$ D、 $x^{2} + x + \frac{1}{4} = 0$

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{36} = \pm 6$ B、 $4 \sqrt{2} \div 2 \sqrt{2}$ $= 2 \sqrt{2}$ C、 $8 \sqrt{3} - 2 \sqrt{6}$ $= 6$ D、 $\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}$ ( $a$ ≥0， $b$ ≥0)

查看试题解析
6. 一组数据：1，3，2，5，x的平均数是3，则这组数据的标准差为（）

A、 2 B、 4 C、 $\sqrt{2}$ D、 -2

查看试题解析
7. 下列给出的四个命题：
①若 $| a | = | b |$ ，则 $a | a | = b | b |$ ；②若 $a^{2} - 5 a + 5 = 0$ ，则 $\sqrt{{(1 - a)}^{2}} = a - 1$ ；
③ $(a - 1) \sqrt{\frac{1}{1 - a}} = \sqrt{1 - a}$ ；
④若方程 $x^{2} + p x + q = 0$ 的两个实数根中有且只有一个根为0，那么 $p \neq 0 ， q = 0$ .
其中是真命题是（）

A、①② B、②③ C、②④ D、③④

查看试题解析
8. 关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根为0，则a的值为（）

A、1 B、－1 C、1或－1 D、 $\frac{1}{2}$

查看试题解析
9. 某农机厂四月份生产零件50万个，第二季度共生产零件182万个．设该厂第二季度平均每月的增长率为 $x$ ，那么 $x$ 满足的方程是（）

A、 $50 {(1 + x)}^{2} = 182$ B、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 182$ C、 $50 (1 + x) + 50 {(1 + x)}^{2} = 182$ D、 $50 + 50 (1 + x) = 182$

查看试题解析
10.
如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形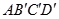，图中阴影部分的面积为（）

A、 $\frac{1}{2}$ B、 $1 - \frac{\sqrt{5}}{4}$ . C、 $\frac{\sqrt{3}}{3}$ D、 $1 - \frac{\sqrt{3}}{3}$

查看试题解析

二、填空题

11.
要使二次根式有意义，x的取值范围是．

查看试题解析
12. 写出一个有两个相等实数根的一元二次方程：．

查看试题解析
13. 某校体育期末考核“立定跳远”、“800米”、“仰卧起坐”三项，并按3： 5：2的比重算出期末成绩．已知小林这三项的考试成绩分别为80分、90分、100分，则小林的体育期末成绩为分．

查看试题解析
14. 设 $a = \sqrt{7}$ ， $b = 2 + \sqrt{3}$ ， $c = \frac{1}{\sqrt{3} - \sqrt{2}}$ ，则 $a$ , $b$ , $c$ 从小到大的顺序是.

查看试题解析
15. 把方程 $x^{2} - 12 x - 3 = 0$ 化为 ${(x + m)}^{2} = n$ ， (其中 $m$ ， $n$ 为常数)的形式后为．

查看试题解析
16.
如图，是一个长为30 $m$ ，宽为20 $m$ 的长方形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532 $m^{2}$ ，那么小道进出口的宽度应为 $m$ ．

查看试题解析
17. 当1≤x≤5时， $\sqrt{{(x - 1)}^{2}} + | x - 5 | =$ ．

查看试题解析
18. 当x取时， $\sqrt{10 + 2 x}$ 的值最小，最小值是；当x取时，2－ $\sqrt{5 - x}$ 的值最大，最大值是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{8} + \sqrt{32} - \sqrt{2}$

(2)、 $(\sqrt{5} - 2) (2 + \sqrt{5})$ $- {(- \sqrt{3})}^{2} + \sqrt{8} \times \frac{1}{\sqrt{2}}$

查看试题解析
20. 解下列一元二次方程：

(1)、x²﹣5x+1=0；

(2)、3（x﹣2）²=x（x﹣2）．

查看试题解析
21. 八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算甲队的平均成绩和方差；

(3)、已知乙队成绩的方差是1 $分^{2}$ ，则成绩较为整齐的是哪一队．

查看试题解析
22. 完成下列问题：

(1)、若 $n (n \neq 0)$ 是关于 $x \geq 0$ 的方程 $x^{2} + m x + 2 n = 0$ 的根，求 $m + n$ 的值；

(2)、已知 $x \geq 0$ ， $y$ 为实数，且 $y =$ $\sqrt{2 x - 5}$ $+ \sqrt{5 - 2 x}$ $- 3$ ，求2xy的值．

查看试题解析
23. 为迎接G20杭州峰会的召开，某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动．了解到某商店正好有这种T恤衫的促销，当购买10件时每件140元，购买数量每增加1件单价减少1元；当购买数量为60件(含60件)以上时，一律每件80元．

(1)、如果购买 x 件(10＜x＜60)，每件的单价为 $y$ 元，请写出 $y$ 关于 $x \geq 0$ 的函数关系式；

(2)、如果八(1)(2)班共购买了100件T恤衫，由于某种原因需分两批购买，且第一批购买量多于30件且少于60件．已知购买两批T恤衫一共花了9200元，求第一批T恤衫的购买数量．

查看试题解析
24.
如图，在边长为12cm的等边三角形ABC中，点P从点A开始沿AB边向点B以每秒钟1cm的速度移动，点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动。若P、Q分别从A、B同时出发，其中任意一点到达目的地后，两点同时停止运动，求：

(1)、经过6秒后，BP= cm，BQ=cm；

(2)、经过几秒后，△BPQ是直角三角形？

(3)、经过几秒△BPQ的面积等于 $10 \sqrt{3}$ cm²?

查看试题解析

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9