江苏省泰兴市黄桥东区域2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2018-12-03 类型：期中考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在实数0， $\frac{22}{7}$ ， $\sqrt{2}$ ， $π$ ，1.010010001……中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列各式表示正确的是（）

A、 $\sqrt{4}$ =±2 B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、± $\sqrt{4}$ =2 D、 $- \sqrt{4} = - 2$

查看试题解析
4. 有一个数值转换器，原理如下：
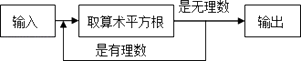
当输入的x=64时，输出的值是（）

A、2 B、8 C、 $\sqrt{2}$ D、 $\sqrt{8}$

查看试题解析
5. 如图，AB∥CD，AD∥BC，EF过点O，图中全等三角形共有（）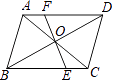

A、2对 B、4对 C、6对 D、8对

查看试题解析
6. 如图，在△ABC中，∠ABC=45°，AD，BE分别为BC，AC边上的高，AD，BE相交于点F，连接CF，则下列结论：①BF=AC；②∠FCD=45°；③若BF=2EC，则△FDC周长等于AB的长；其中正确的有（）

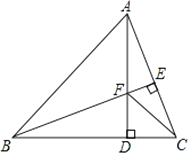A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

7. $- \sqrt{5}$ 的绝对值是 .

查看试题解析
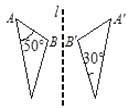
8. 如图，△ABC与△A′B′C′关于直线 $l$ 对称，则∠B的度数为°

查看试题解析
9. 我国“辽宁号”航空母舰的满载排水量为67500吨，将数据67500精确到千位的近似值为．（结果用科学记数法表示）

查看试题解析
10. 比较大小： $\sqrt{10}$ ＋14（填“＞”、“＜”或“＝”）．

查看试题解析
11. 如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径画弧，交AC于点D，连接BD，则∠DBC等于°

查看试题解析
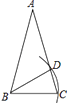12. 下列说法：①如果两个三角形全等，那么这两个三角形一定成轴对称；②数轴上的点和实数一一对应；③ $\sqrt{3}$ 是3的一个平方根；④两个无理数的和一定为无理数；⑤6.9 $\times$ 10³精确到十分位；⑥ $\sqrt{16}$ 的平方根是 $\pm$ 4.其中正确的.（填序号）

查看试题解析
13. 如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为.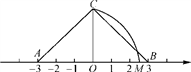

查看试题解析
14. 如图，∠AOB=45°，点M，N在边OA上，OM=3，ON=7，点P是直线OB上的点，要使点P，M，N构成等腰三角形的点P有个．

查看试题解析
15. 如图，在等边三角形ABC中，AC＝9，点O在AC上，且AO＝3，点P是AB上的一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是．

查看试题解析

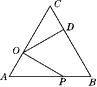
三、解答题

16. 等腰三角形的两边分别为3和6，则这个三角形的周长是多少？

查看试题解析
17. 计算： $\sqrt{9} - 2^{- 1} + \sqrt[3]{8} - | \sqrt{3} - 3 |$ ；

查看试题解析
18. 求x的值： ${(x + 2)}^{2}$ ＝9．

查看试题解析
19. 已知实数 $x 、 y 、 m$ 满足 $\sqrt{x + 2} + | 3 x + y + m | = 0$ ，且 $y$ 是负数，求 $m$ 取值范围。

查看试题解析
20. 如图，点A、B分别表示2个居民小区.

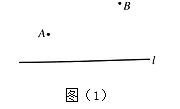
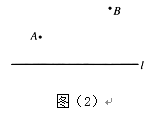(1)、若直线 $l$ 表示公交通道，欲在公交通道旁建1个公交车站P，使该站到2个小区的距离相等，应如何确定车站的位置？请在图（1）中画出，尺规作图，保留痕迹；

(2)、若直线 $l$ 表示自来水总水管，欲在自来水总管道旁建1个加压站P，使该站向2个小区送水的管道总长度最短，应如何确定加压站的位置？请在图（2）中画出.

查看试题解析
21. 方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图①，△ABC是格点三角形．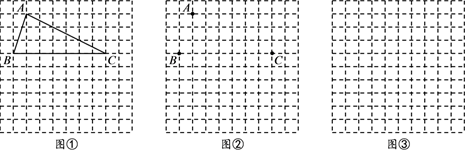

(1)、试在图②中确定格点D，画一个以A、B、C、D为顶点的四边形，使其为轴对称图形（画出一个即可），并写出你画的图形的面积 .

(2)、试在图③中画一个“格点正方形”，使其面积等于10．

查看试题解析
22. 如图，在等边△ABC中，E，F分别在边AC、BC上，满足AE＝CF，连接BE，AF交于点P．

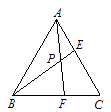(1)、求证：△ABE≌△CAF；

(2)、求∠APB的度数．

查看试题解析
23. 如图，在△ABC中，AC＝21，BC＝13，D是AC边上一点，BD＝12，AD＝16，

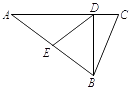(1)、若E是边AB的中点，求线段DE的长

(2)、若E是边AB上的动点，求线段DE的最小值．

查看试题解析
24. 如图，在△ABC中，点P是BC上一点，PR⊥AB，PS⊥AC，垂足分别为点R、S，PR=PS，点Q是AC上一点，且AQ=PQ，

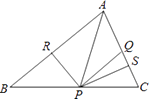(1)、求证：QP∥AR；

(2)、AR、AS相等吗？说明理由.

查看试题解析
25. 在△ABC中，AB、AC边的垂直平分线分别交BC边于点M、N．

(1)、如图①，若△AMN是等边三角形，则∠BAC=°；

(2)、如图②，若∠BAC=135°，求证：BM²＋CN²＝MN² ．

(3)、如图③，∠ABC的平分线BP和AC边的垂直平分线相交于点P，过点P作PH垂直BA的延长线于点H．若AB=4，CB=10，求AH的长．

查看试题解析
26.

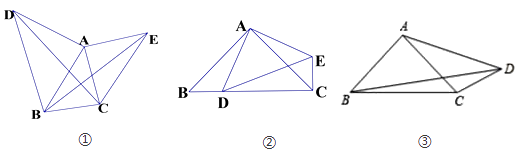
(1)、【问题探究】如图①已知锐角△ABC，分别以AB、AC为腰，在△ABC的外部作等腰Rt△ABD和Rt△ACE，连接CD、BE，是猜想CD、BE的大小关系；（不必证明）

(2)、【深入探究】如图②△ABC、△ADE都是等腰直角三角形，点D在边BC上（不与B、C重合），连接EC，则线段BC，DC，EC之间满足的等量关系式为；（不必证明）线段AD² ， BD² ， CD²之间满足的等量关系，并证明你的结论；

(3)、【拓展应用】如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD的长．

查看试题解析