江苏省如皋市南片区八校联考2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-12-03 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中,计算结果正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、a3+a3=2a3 D、(a2b)2=a2b23. 下列各式由左到右的变形中,属于因式分解的是( )A、a(m+n)=am+an B、a2﹣b2﹣c2=(a﹣b)(a+b)﹣c2 C、10x2﹣5x=5x(2x﹣1) D、x2﹣16+6x=(x+4)(x﹣4)+6x4. 如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
2. 下列运算中,计算结果正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、a3+a3=2a3 D、(a2b)2=a2b23. 下列各式由左到右的变形中,属于因式分解的是( )A、a(m+n)=am+an B、a2﹣b2﹣c2=(a﹣b)(a+b)﹣c2 C、10x2﹣5x=5x(2x﹣1) D、x2﹣16+6x=(x+4)(x﹣4)+6x4. 如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )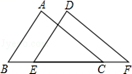 A、AC=DF B、AC∥DF C、∠A=∠D D、∠ACB=∠F5. 若x2+kx+81是一个完全平方式,则k的值为( )A、18 B、﹣18 C、±9 D、±186. 若 ,则 的值为( )A、-5 B、-2 C、5 D、27. 已知 ,则 的值是( )A、1 B、5 C、7 D、98. 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
A、AC=DF B、AC∥DF C、∠A=∠D D、∠ACB=∠F5. 若x2+kx+81是一个完全平方式,则k的值为( )A、18 B、﹣18 C、±9 D、±186. 若 ,则 的值为( )A、-5 B、-2 C、5 D、27. 已知 ,则 的值是( )A、1 B、5 C、7 D、98. 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( ) A、50° B、45° C、55° D、60°9. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为( )
A、50° B、45° C、55° D、60°9. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为( ) A、3 B、4 C、2 D、2.510. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A、3 B、4 C、2 D、2.510. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )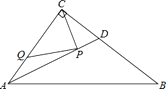 A、2.4 B、4.8 C、4 D、5
A、2.4 B、4.8 C、4 D、5二、填空题
-
11. 计算:a•a2•a3= .12. 因式分解: = .13. 已知点A(m,3)与点B(2,n)关于x轴对称,则m+n= .14. 若(a﹣1)0=1,则a的取值范围是 .15. 如图,点B、A、E在同一直线上,△ADB≌△ACE,∠E=40°,∠C=25°,则∠DAC=°
 16. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是18cm2 , AB=10cm,AC=8cm,则DE= .
16. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是18cm2 , AB=10cm,AC=8cm,则DE= .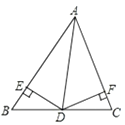 17. 如图,在△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E.如果AD=1,BC=6,那么CE等于 .
17. 如图,在△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E.如果AD=1,BC=6,那么CE等于 .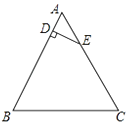 18. 如图,在 中,AB=AC,∠BAC=90 ,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE=∠CPF;(3)△EPF是等腰直角三角形;(4) = (5)EF=AP其中一定成立的有个.
18. 如图,在 中,AB=AC,∠BAC=90 ,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE=∠CPF;(3)△EPF是等腰直角三角形;(4) = (5)EF=AP其中一定成立的有个.
三、解答题
-
19. 计算:
(1)、(15x2y﹣10xy2)÷(﹣5xy);(2)、(m+2n+3)(m+2n﹣3).20. 分解因式:
(1)、-3x2+6xy-3y2;(2)、 .21. 先化简,再求值: ,其中x=1,y=2.22. 如图,AC=AE,BC=DE,AB=AD.求证:∠1=∠2. 23. 如图,已知A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(5,2)
23. 如图,已知A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(5,2)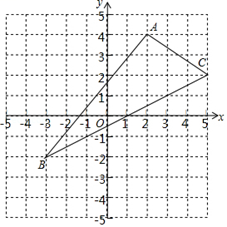 (1)、在图中画出△ABC关于y轴对称的△A′B′C′,写出点A′,B′,C′的坐标;(2)、求△ABC的面积;24. 如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
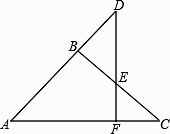
(1)、在图中画出△ABC关于y轴对称的△A′B′C′,写出点A′,B′,C′的坐标;(2)、求△ABC的面积;24. 如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,求证:△DBE是等腰三角形.
 25. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
25. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.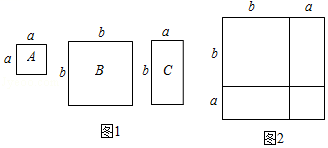 (1)、请用两种不同的方法求图2大正方形的面积.(2)、观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系.(3)、根据(2)题中的等量关系,解决如下问题:
(1)、请用两种不同的方法求图2大正方形的面积.(2)、观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系.(3)、根据(2)题中的等量关系,解决如下问题:①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
26. 已知:如图1,在平面直角坐标系中,点A,B,C都在坐标轴上,且OA=OB=OC,△ABC的面积为9,点P从C点出发沿y轴负方向以1个单位/秒的速度向下运动,连接PA,PB,D(﹣m,﹣m)为AC上的点(m>0)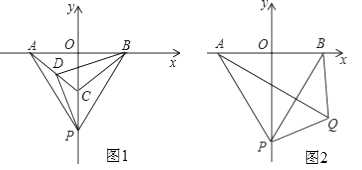 (1)、试分别求出A,B,C三点的坐标;(2)、设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?请说明理由;(3)、如图2,若PA=AB,在第四象限内有一动点Q,连QA,QB,QP,且∠PQA=60°,当Q在第四象限内运动时,求∠APQ与∠PBQ的度数和.
(1)、试分别求出A,B,C三点的坐标;(2)、设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?请说明理由;(3)、如图2,若PA=AB,在第四象限内有一动点Q,连QA,QB,QP,且∠PQA=60°,当Q在第四象限内运动时,求∠APQ与∠PBQ的度数和.