2018-2019学年数学浙教版九年级上册4.5 相似三角形的性质及其应用（2） 同步练习
试卷更新日期：2018-12-03 类型：同步测试
一、选择题
-
1. 如图，路灯AB的高度为8米，树CD与路灯的水平距离为4米，则得树在灯光下的影长DE为3米，则树高（ ）
A、4米 B、6米 C、 米 D、 米2. 如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射到桌面后在地面上形成（圆形）的示意图. 已知桌面直径为1.2米，桌面离地面1米. 若灯泡离地面3米，则地面上阴影部分的面积为（ ）
A、0.36π米2 B、0.81π米2 C、2π米2 D、3.24π米23.如图是一个照相机成像的示意图，如果底片AB宽40mm，焦距是60mm，所拍摄的2m外的景物的宽CD为（ ）
A、12m B、3m C、m D、m4. 如图是一束平行的光线从教室窗户射入教室的平面示意图，测得光线与地面所成的角 ，窗户的高在教室地面上的影长 米，窗户的下檐到教室地面的距离 米（点 、 、 在同一直线上），则窗户的高 为（ ）
A、 米 B、3米 C、2米 D、1.5米5. 志远要在报纸上刊登广告，一块10cm×5cm的长方形版面要付广告费180元，他要把该版面的边长都扩大为原来的3倍，在每平方厘米版面广告费相同的情况下，他该付广告费（ ）
A、540元 B、1080元 C、1620元 D、1800元6. 如图，小明在 时测得某树的影长为 ， 时又测得该树的影长为 ，若两次日照的光线互相垂直，则树的高度为（ ）m．
A、2 B、4 C、6 D、8二、填空题
-
7. 在某天的同一时刻，高为 的小明的影长为 ，烟囱的影长为 ，则这座烟囱的高为 ．8. 如图所示， 是一个平面镜，光线从 点射出经过 上的 点反射后照射到 点，设入射角为 （入射角等于反射角）， ， ，垂足分别为点 ， ．若 ， ， ，则 = ．
9. 如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=m．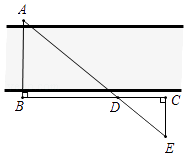
10. “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学
九章算术 
中的“井深几何”问题，它的题意可以由图获得，则井深为尺
11. 如图，一条 宽的道路将矩形花坛分为一个直角三角形和一个直角梯形，根据图中数据，可知这条道路的占地面积为 ．
三、解答题
-
12. 如图，一位测量人员，要测量池塘的宽度 的长，他过 两点画两条相交于点 的射线，在射线上取两点 ，使 ，若测得 米，他能求出 之间的距离吗？若能，请你帮他算出来；若不能，请你帮他设计一个可行方案．
13. 如图，取一根9.5m长的标杆AB，在其上系一活动旗帜C，使标杆的影子落在平地和一堤坝的左斜坡上，拉动旗帜使其影子正好落在斜坡底角顶点D处．若测得旗高BC＝4.5m，影长BD＝9m，影长DE＝5m，请计算左斜坡的坡比(假设标杆的影子BD，DE均与坝底线DM垂直)．
14. 如图，一条东西走向的笔直公路，点A、B表示公路北侧间隔150米的两棵树所在的位置，点C表示电视塔所在的位置．小王在公路PQ南侧直线行走，当他到达点P的位置时，观察树A恰好挡住电视塔，即点P、A、C在一条直线上，当他继续走180米到达点Q的位置时，以同样方法观察电视塔，观察树B也恰好挡住电视塔．假设公路两侧AB∥PQ，且公路的宽为60米，求电视塔C到公路南侧PQ的距离．
15. 如图所示，竖杆AC、BD的长度分别为200cm、300cm，CD=300cm．现有一男生站在斜杆AB下方的点E处，设CE=x（cm），从E处跳起的摸高EF=y（cm）．
(1)、求y与x之间的函数关系式；(2)、若245（cm）≤y＜255（cm）时，求该男生跳起时站的位置x（cm）的范围．