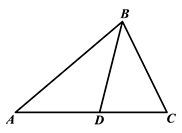2018-2019学年数学浙教版九年级上册4.5 相似三角形的性质及其应用(1) 同步练习
试卷更新日期:2018-12-03 类型:同步测试
一、选择题
-
1. 已知△ABC∽△DEF,且相似比为2∶1,若△ABC的周长是8 cm,则△DEF的周长是( )A、2 cm B、4 cm C、8 cm D、16 cm2. 两相似三角形的周长之比为1:4,那么他们的对应边上的高的比为( )
A、1∶4 B、1∶2 C、2∶1 D、 ∶23. 若 的各边都分别扩大到原来的2倍,得到 ,下列结论正确的是( )
A、 与 的对应角不相等 B、 与 不一定相似 C、 与 的相似比为1:2 D、 与 的相似比为2:14. 如图,在△ABC中,D,E两点分别在BC,AD上,且AD为∠BAC的角平分线,若∠ABE = ∠C,AE:ED=2:1,则△BDE与△ABC的面积之比为( ) A、1:6 B、1:9 C、2:13 D、2:155. 如图,点D、E分别为△ABC的边AB、AC上的中点,则四边形BCED的面积与△ADE的面积的比为( )
A、1:6 B、1:9 C、2:13 D、2:155. 如图,点D、E分别为△ABC的边AB、AC上的中点,则四边形BCED的面积与△ADE的面积的比为( ) A、2:1 B、3:1 C、4:1 D、1:16. 如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,记与点A重合的点为A′,则 A′BG的面积与该矩形面积的比为( )
A、2:1 B、3:1 C、4:1 D、1:16. 如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,记与点A重合的点为A′,则 A′BG的面积与该矩形面积的比为( )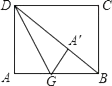 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 与 相似且对应中线的比为3:5,则 与 面积的比为 .8. 已知△ABC∽△A1B1C1 , △ABC的周长与△A1B1C1的周长的比值是 ,BE、B1E1分别是它们对应边上的中线,且BE=6,则B1E1= .
9. 一只蚂蚁沿着直角三角形的边爬行一周需 ,如果将直角三角形的边长扩大到原来的2倍,那么这只蚂蚁再沿边爬行一周需 .
10. 如图,在平行四边形ABCD中,点E是CD边上一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F.若S△DEF=2,则S△ABE= . 11. 如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S□ABCD= .
11. 如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S□ABCD= .
三、解答题
-
12. 如图,已知DE∥BC,CD与BE相交于点O,并且S△DOE:S△COB=4:9,
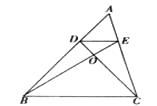 (1)、求AE:AC的值;(2)、求△ADE与四边形DBCE的面积比。
(1)、求AE:AC的值;(2)、求△ADE与四边形DBCE的面积比。