2018-2019学年数学浙教版九年级上册4.4 两个三角形相似的判定(1) 同步练习
试卷更新日期:2018-12-03 类型:同步测试
一、选择题.
-
1. 如图,在平行四边形 中,E是AB延长线上一点,连接 ,交 于点 ,交 于点 ,那么图中相似三角形(不含全等三角形)共有( )
 A、6对 B、5对 C、4对 D、3对2. 如图,在▱ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( )
A、6对 B、5对 C、4对 D、3对2. 如图,在▱ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( ) A、 B、 C、 D、3. 如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=9:16,则DE:BC为( )
A、 B、 C、 D、3. 如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=9:16,则DE:BC为( ) A、2:3 B、3:4 C、9:16 D、1:24. 如图, 是矩形 的 边上任意一点, 是 边上一点, ,图中一定相似的三角形是( )
A、2:3 B、3:4 C、9:16 D、1:24. 如图, 是矩形 的 边上任意一点, 是 边上一点, ,图中一定相似的三角形是( ) A、①与② B、③与④ C、②与③ D、①与④5. 如图,△ABC中,AD是中线,BC=4,∠B=∠DAC,则线段AC的长为( )
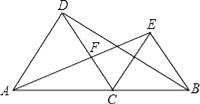
A、①与② B、③与④ C、②与③ D、①与④5. 如图,△ABC中,AD是中线,BC=4,∠B=∠DAC,则线段AC的长为( )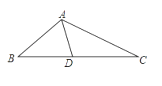 A、 B、2 C、3 D、6. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A、 B、2 C、3 D、6. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )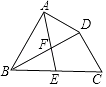 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 . (只需写一个条件,不添加辅助线和字母)
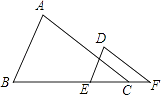 8. 如图,已知AB∥CD,若 ,则 = .
8. 如图,已知AB∥CD,若 ,则 = . 9. 如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD= .
9. 如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD= . 10. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .
10. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .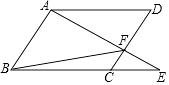 11. 如图,△ABC中,AC=3,BC=4,AB=5,线段DE⊥AB,且△BDE的面积是△ABC面积的三分之一,那么,线段BD长为 .
11. 如图,△ABC中,AC=3,BC=4,AB=5,线段DE⊥AB,且△BDE的面积是△ABC面积的三分之一,那么,线段BD长为 .
三、解答题
-
12. 如图,四边形 是正方形,点 在 上, 于 ,求证:△DAF∽△AEB.