2018-2019学年数学浙教版九年级上册4.1成比例线段（3）同步练习

试卷更新日期：2018-12-03 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，AB∥CD，AD与BC相交于点P，AB=3，CD=6，AP=4，则DP的长为（）

A、3 B、4 C、6 D、8

查看试题解析
2. 如图，DE∥FG∥BC，若DB=4FB，则EG与GC的关系是（）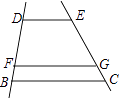

A、EG=4GC B、EG=3GC C、EG= $\frac{5}{2}$ GC D、EG=2GC

查看试题解析
3. 如图，在△ABC中，点D、E分别在AB、AC边上，且DE∥BC，若 $\frac{A D}{D B}$ = $\frac{3}{2}$ ，则 $\frac{A E}{A C}$ 的值等于（）

A、 $\frac{3}{2}$ B、3 C、 $\frac{2}{3}$ D、 $\frac{3}{5}$

查看试题解析
4. 如图，DE∥BC，且DB=AE，若AB=5，AC=10，则AE的长为（）

A、2 B、2.5 C、 $\sqrt{10}$ D、 $\frac{10}{3}$

查看试题解析
5. 如图，l₁∥l₂∥l₃ ，则下列等式错误的是（）

A、 $\frac{B C}{A C} = \frac{E F}{D F}$ B、 $\frac{A B}{A C} = \frac{D E}{D F}$ C、 $\frac{A B}{D E} = \frac{B C}{E F}$ D、 $\frac{A B}{A C} = \frac{A D}{C F}$

查看试题解析
6. 如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（）

A、 $\frac{A D}{D F} = \frac{B C}{C E}$ B、 $\frac{A G}{G D} = \frac{B G}{C G}$ C、 $\frac{G C}{G E} = \frac{C D}{E F}$ D、 $\frac{A B}{E F} = \frac{A G}{G E}$

查看试题解析
7.
如图，点A在双曲线y= $\frac{3}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（）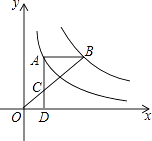

A、6 B、9 C、10 D、12

查看试题解析
8. 如图，AD∥BC，AD⊥AB，点A，B在y轴上，CD与x轴交于点E（2，0），且AD=DE，BC=2CE，则BD与x轴交点F的横坐标为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{5}{6}$

查看试题解析

二、填空题

9. 如图，在△ABC中，若DE∥BC， $\frac{A D}{D B}$ = $\frac{2}{3}$ ，DE=4，则BC的长是．

查看试题解析
10.

(1)、三条平行线截两条直线，所得的的比相等．

(2)、平行于三角形一边的直线截其他两边（或两边的延长线），所得的相等．

(3)、平行于三角形一边的直线和其他两边（或两边的延长线）相交，所得的三角形与原三角形．

查看试题解析
11. 如图，已知DE∥BC，AE=2，EC=6，AB=5，则AD= ．

查看试题解析
12. 如图，AD∥BE∥CF，直线l₁ ， l₂与这三条平行线分别交于点A，B，C和点D，E，F， $\frac{A B}{B C}$ = $\frac{2}{3}$ ，DE=6，则EF= ．

查看试题解析
13. 如图，△ABC中，AF：FD=1：2，BD=DC，则EF：BF= ．

查看试题解析
14. 已知AM是△ABC中BC边上的中线，P是△ABC的重心，过P作EF（EF∥BC），分别交AB、AC于E、F，则 $\frac{B E}{A E} + \frac{C F}{A F}$ = ．

查看试题解析
15. 如图，△ABC的面积为S．点P₁ ， P₂ ， P₃ ， …，P_n_﹣1是边BC的n等分点（n≥3，且n为整数），点M，N分别在边AB，AC上，且 $\frac{A M}{A B}$ = $\frac{A N}{A C}$ = $\frac{1}{n}$ ，连接MP₁ ， MP₂ ， MP₃ ， …，MP_n_﹣1 ，连接NB，NP₁ ， NP₂ ， …，NP_n_﹣1 ，线段MP₁与NB相交于点D₁ ，线段MP₂与NP₁相交于点D₂ ，线段MP₃与NP₂相交于点D₃ ， …，线段MP_n_﹣1与NP_n_﹣2相交于点D_n_﹣1 ，则△ND₁P₁ ， △ND₂P₂ ， △ND₃P₃ ， …，△ND_n_﹣1P_n_﹣1的面积和是．（用含有S与n的式子表示）

查看试题解析

三、解答题

16. 已知：如图，在△ABC中，DE∥BC，AD=3，DB=5，AE=2，求AC的长．

查看试题解析
17. 如图．在△ABC中，E是AB的中点，D是AC上的一点，且AD：DC=2：3，BD与CE交于F，S_△_AB_C=40，求S_AEFD ．

查看试题解析
18. 如图，D在AB上，且DE∥BC交AC于E，F在AD上，且AD²=AF•AB．
求证：EF∥CD．

查看试题解析
19. 如图，过▱ABCD的顶点A的直线交BD于点P，交CD于点Q，交BC的延长线于点R．
求证： $\frac{P Q}{P R} = \frac{P D^{2}}{P B^{2}}$ ．

查看试题解析
20. 如图，D，E两点是线段AC上的点，且AD=DE=EC．

(1)、分别过D，E画出BC的平行线，分别交AB于F，G两点；

(2)、量一量线段AF，FG，GB的长度，你能得出什么结论？

查看试题解析
21. 如图，已知△ABC中，AC=BC，F为底边AB上一点，BF：AF=m：n（m＞0，n＞0），取CF的中点D，连结AD并延长交BC于E．求BE：EC的值．

查看试题解析

2018-2019学年数学浙教版九年级上册4.1成比例线段（3） 同步练习

一、选择题

二、填空题

三、解答题

2018-2019学年数学浙教版九年级上册4.1成比例线段（3）同步练习