浙江省丽水市2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期：2018-12-03 类型：期中考试
一、 单选题
-
1. 抛物线y=-(x-1) 2 +2的顶点坐标是（ ）
A、(1，2) B、(－1，2) C、(1，－2) D、(－1，－2)2. 如图，任意转动正六边形转盘一次，当转盘停止转动时，指针指向大于3的数的概率是（ ）
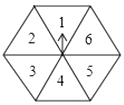
A、 B、 C、 D、3. 如图，点A，B，C在⊙O上，若∠BOC=72°，则∠BAC的度数是（ ）
A、72° B、36° C、18° D、54°4. 下列函数中，是二次函数的是（ ）A、y=- B、y=2x2-x-1 C、y= D、y=x+25. 在圆内接四边形ABCD中，∠A∶∠B∶∠C∶∠D的度数之比可能是（ ）
A、1∶2∶3∶4 B、4∶2∶1∶3 C、4∶2∶3∶1 D、1∶3∶2∶46. 布袋中有红、黄、蓝三种颜色的球各一个，从中摸出一个球之后不放回布袋，再摸第二个球，这时得到的两个球的颜色中有“一红一黄”的概率是（ ）
A、 B、 C、 D、7. 已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：x
－1
0
1
3
y
－3
1
3
1
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1；③当x<1时，函数值y随x的增大而增大；④方程ax2+bx+c=0有一个根大于4，其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，A，B，C是⊙O上三个点，∠AOB=2∠BOC，则下列说法中正确的是（ ）
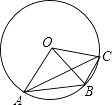A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°9. 若二次函数y=x2-6x+9的图象经过A(－1，y1)，B(1，y2)，C(3+ ，y3)三点．则关于y1 ， y2 ， y3大小关系正确的是（ ）
A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y3>y1>y210. 如图，⊙O的外切正六边形ABCDEF的边长为2，则图中阴影部分的面积为（ ）
A、 B、 C、 D、二、填空题
-
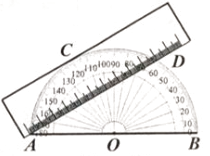
11. 抛物线y=(x-1)2-2与y轴的交点坐标是12. 一只不透明的袋子里装有4个黑球，2个白球，每个球除颜色外都相同，则事件“从中任意摸出3个球，至少有1个球是黑球”属于事件．（填写“必然”，“不可能”或“随机”）13. 如图，量角器的0度刻度线为AB，将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A，D，量得AD=10cm，点D在量角器上的读数为60°，则该直尺的宽度为 cm。
14. 抛物线y=ax2+bx+c经过点A(－5，4)，且对称轴是直线x=－2，则a+b+c=
15. 如图，一抛物线型拱桥，当拱顶到水面的距离为2米时，水面宽度为4米；那么当水位下降1米后，水面的宽度为米．
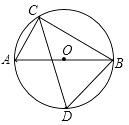
16. 如图，△ABC内接于⊙O，∠ACB=90°，∠ACB的角平分线交⊙O于D．若AC=6，BD= ，则BC的长为。
三、解答题
-
17. 已知抛物线y=ax2+bx-3(a≠0)经过点(－1，0)，(3，0)，求a，b的值
18. 一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外都相同，其中红球有1个，若从中随机摸出一个球，这个球是白球的概率为(1)、求袋子中白球的个数；（请通过列式或列方程解答）(2)、随机摸出一个球后，不放回，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）19. 如图，已知OA、OB、OC是⊙O的三条半径，点C是弧AB的中点，M、N分别是OA、OB的中点．求证：MC=NC．
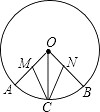
20. 已知抛物线y=－x2＋2x＋3．
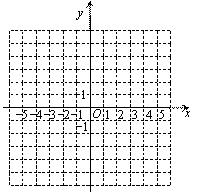(1)、求该抛物线的对称轴和顶点P的坐标．(2)、在图中的直角坐标系内用五点法画出该抛物线的图象(3)、将该抛物线向下平移2个单位，向左平移3个单位得到抛物线y1 ， 此时点P的对应点为P′，试求直线PP′与y轴的交点坐标21. 商场销售一批衬衫，每天可售出20件，每件可盈利40元．为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一件衬衫每降价1元，每天可多售出2件．
(1)、设每件降价x元，每天盈利y元，写出y与x之间的函数关系式．
(2)、若商场每天要盈利1200元，每件衬衫降价幅度不能超过18元，那么每件衬衫应降价多少元？
(3)、每件衬衫降价多少元时，商场每天的盈利能达到最大，盈利最大是多少元？
22. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，延长DC交AB的延长线于点E．
(1)、若∠ADC=86°，求∠CBE的度数；(2)、若AC=EC，求证：AD=BE23. 今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表
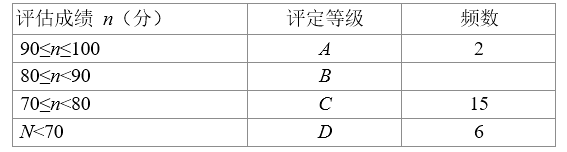
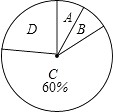
根据以上信息解答下列问题：
(1)、求m的值；(2)、在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）(3)、从评估成绩不少于 80 分的连锁店中任选 2 家介绍营销经验， 求其中至少有一家是 A 等级的概率．
24. 如图，在平面直角坐标系中，二次函数的图象交坐标轴于A(－1，0)，B(4，0)，C(0，－4)三点，点P是直线BC下方抛物线上一动点．
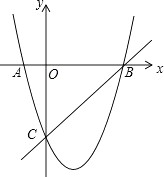(1)、求这个二次函数的解析式；(2)、是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；(3)、动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．