人教版八年级数学上册 13.3.2等边三角形（一） 同步练习
试卷更新日期：2018-12-03 类型：同步测试
一、选择题
-
1. 一个三角形任意一边上的高都是这边上的中线，则对这个三角形最准确的判断是（ ）A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形2. 已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1 ， O，P2三点所构成的三角形是（ ）A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形3. 在△ABC中，∠A=∠B=∠C，过点B作BD⊥AC于D，已知△ABC的周长为m，则AD=（ ）A、 B、 C、 D、4. 如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）
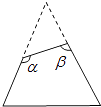A、180° B、220° C、240° D、300°5. 已知下列命题：①若 ＞1，则a＞b；②若a+b=0，则|a|=|b|；③等边三角形的三个内角都相等；④底角相等的两个等腰三角形全等．其中原命题与逆命题均为真命题的个数是（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，l∥m，等边△ABC的顶点B在直线m上，∠1=20°，则∠2的度数为（ ）
A、60° B、45° C、40° D、30°7. 如图，在四边形ABCD中，AC ， BD为对角线，AB＝BC＝AC＝BD ， 则∠ADC的大小为（ ）
A、120° B、135° C、145° D、150°8. 如图，∠AOB=60°，OA=OB，动点C从点O出发，沿射线OB方向移动，以AC为边在右侧作等边△ACD，连接BD，则BD所在直线与OA所在直线的位置关系是（ ）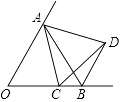
A、平行 B、相交 C、垂直 D、平行、相交或垂直二、填空题
-
9. 如图，△ABC是等边三角形，AD⊥BC，垂足为D，则∠BAD= ， BD=AB．
10. 等边三角形的周长是30cm，一边上的高是5 cm，则该三角形的面积为 cm2 ．11. 如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是度．
12. 如图，已知直线l1∥l2 ， 将等边三角形如图放置，若∠α=40°，则∠β等于 ．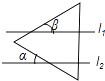
13. 如图，在△ABC中，按以下步骤作图：①分别以点A和点C为圆心，以大于 AC的长为半径作弧，两弧相交于M、N两点；②作直线MN交BC于点D，连接AD．若AB=BD，AB=6，∠C=30°，则△ACD的面积为 ．
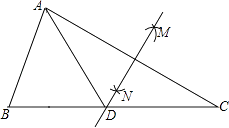14. 如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE=1，∠E=30°，则BC= ．
15. 如图，在平面直角坐标系中，△AA1C1是边长为1的等边三角形，点C1在y轴的正半轴上，以AA2=2为边长画等边△AA2C2；以AA3=4为边长画等边△AA3C3 ， …，按此规律继续画等边三角形，则点An的坐标为 ．
三、解答题
-
16. 如图，△ABD、△AEC都是等边三角形，求证：BE=DC．
17. 已知：在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF．求证：△ABC是等边三角形．
18. 如图，C为线段AE上一动点(不与点A、E重合)，在AE同侧分别作等边△ABC和等边△CDE，AD与BC相交于点P，BE与CD相交于点Q，连接PQ.求证：△PCQ为等边三角形．
19. 如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．
20.
(1)、图（1）中，C点为线段AB上一点，△ACM，△CBN是等边三角形，AN与BM相等吗？说明理由；
(2)、如图（2）C点为线段AB上一点，等边三角形ACM和等边三角形CBN在AB的异侧，此时AN与BM相等吗？说明理由；
(3)、如图（3）C点为线段AB外一点，△ACM，△CBN是等边三角形，AN与BM相等吗？说明理由．
21. 如图
(1)、动手操作：如图①，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点c'处，折痕为EF，若∠ABE=20°，那么∠EFC'的度数为 ▲ ．
(2)、观察发现：小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．
(3)、实践与运用：将矩形纸片ABCD按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP=MN=PQ（如图④），求∠MNF的大小．