人教版八年级数学上册 13.3.2等边三角形（二） 同步练习
试卷更新日期：2018-12-03 类型：同步测试
一、选择题
-
1. 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE的长为（ ）
A、10 B、8 C、5 D、2.52. 如图，△ABC中，∠C=90°，∠A=30°，AB=12，则BC=（ ）
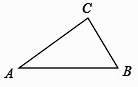A、6 B、6 C、6 D、123. 在△ABC中，∠ACB为直角，∠A=30°，CD⊥AB于D，若BD=1，则AB的长度是（ ）
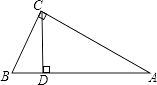A、4 B、3 C、2 D、14. 如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（ ）
A、 m B、4m C、4 m D、8m5. 如图折叠直角三角形纸片的直角，使点C落在斜边AB上的点E处，已知CD=1，∠B=30°，则BD的长是（ ）
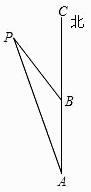
A、1 B、2 C、 D、26. 如图，∠AOB=60°，以点O为圆心，以任意长为半径作弧交OA，OB于C，D两点；分别以C，D为圆心，以大于 CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上截取线段OM=6，则M点到OB的距离为（ ）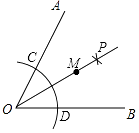
A、6 B、2 C、3 D、7. 如图，把直角三角形ABO放置在平面直角坐标系中，已知 ，B点的坐标为（0，2），将△ABO沿着斜边AB翻折后得到△ABC，则点C的坐标是（ ）
A、 B、 C、 D、8. 已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G．当G与D重合时，AD的长是（ ）A、3 B、4 C、8 D、99. 如图，△ABC为等边三角形，点D，E分别在AC，BC上，且AD＝CE，AE与BD相交于点P，BF⊥AE于点F.若PF＝3，则BP＝（ ）
A、6 B、5 C、4 D、3二、填空题
-
10. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，若BD＝10，则CD＝.
11. 三角形三内角的度数之比为1：2：3，最大边的长是8cm，则最小边的长是cm．12. 如图，△ABC中，∠ACB=90°，CD是高，若∠A=30°，BD=1，则AD=
13. 如图，在四边形ABCD中，∠B=∠D=90°，∠A=60°，AB=4，则AD的取值范围是 ．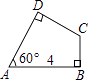
14. 如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB于C，若EC=1，则OF= ．
15. 在等腰△ABC中，AD⊥BC交直线BC于点D，若AD= BC，则△ABC的顶角的度数为 ．三、解答题
-
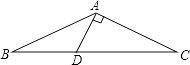
16. 如图，△ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于点D，
求证：BC=3AD．
17. 已知：如图，在Rt△ABC中，∠B=30°，∠C=90°，BD=AD，BD=12.求DC的长．
18. 如图，BE平分∠ABF，DF⊥AB交AB于点D，AC⊥BF交BF于点C，AC，FD相交于点E，若∠F=30°，DE=1，求AC的长．
19. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
(1)、求∠F的度数；(2)、若CD=2，求DF的长．
