人教版八年级数学上册 13.3.1等腰三角形（二） 同步练习
试卷更新日期：2018-12-03 类型：同步测试
一、选择题
-
1. 如图，O是△ABC的∠ABC，∠ACB的平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若△ODE的周长为10厘米，那么BC的长为（ ）
A、8cm B、9cm C、10cm D、11cm2.如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，AB=5，AC=7，BC=8，△AEF的周长为（ ）
A、13 B、12 C、15 D、203. 推理：如图，∵∠A=∠ACD，∠B=∠BCD，（已知）∴AD=CD，CD=DB（ 等腰三角形的性质）∴AD=DB，依据是（ ）
A、旋转不改变图形的大小 B、连接两点的所有线中线段最短 C、等量代换 D、整体大于部分4. 如图，在△ABC中，AB=AC，D、E两点分别在AC、BC上，BD是∠ABC的平分线，DE∥AB，若BE=5cm，CE=3cm，则△CDE的周长是（ ）
A、15cm B、13cm C、11cm D、9cm5. 如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则图中等腰三角形的个数有（ ）
A、1个 B、2个 C、3个 D、4个6. 如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）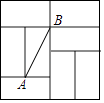
A、2个 B、3个 C、4个 D、5个7. 如图，在 中， ， ，点E在BC的延长线上， 的平分线BD与 的平分线CD相交于点D，连接AD，则下列结论中，正确的是（ ）
A、 B、 C、 D、AC=AB8. 如图，坐标平面内一点A，O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（ ）
A、2 B、3 C、4 D、5二、填空题
-
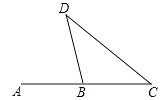
9. 如图，∠ABD=76°，∠C=38°，BC=30cm，则BD的长为 ．
10. 四边形ABCD中，∠A=∠B=90°，AB=AD=4，BC=7．以四边形的一个顶点为顶点画一个腰长为3的等腰三角形，并使得三角形的另两个顶点都在四边形的边上．如果要求画出的三角形形状大小各不相同，则最多可以画出个这样的等腰三角形．11. 如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，则路灯的高为 m．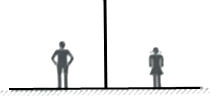
12. 已知，如图，在△ABC中，∠C=90°，∠A=24°，请用直尺和圆规找到一条直线，把△ABC恰好分割成两个等腰三角形（不写作法，但需保留作图痕迹），直线 即为所求．
13. 如图，在△ABC中，AB=AC，D、E两点分别在AC、BC上，BD是∠ABC的平分线，DE∥AB，若BE=5cm，CE=3cm，则△CDE的周长是 ．
14. 如图，在ΔABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是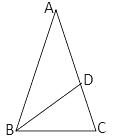
15. 如图，∠ABC，∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论：①△BDF，△CEF都是等腰三角形；
②DE=BD+CE；
③△ADE的周长为AB+AC；
④BD=CE．
其中正确的是 ．
三、解答题
-
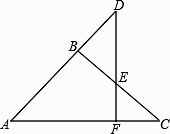
16. 如图，△ABC中BA=BC，点D是AB延长线上一点，DF⊥AC于F交BC于E，
求证：△DBE是等腰三角形．
17. 如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F．
(1)、∠B=∠C．(2)、△ABC是等腰三角形．18. 如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC．求证：△BDE是等腰三角形．
