2016-2017学年河北省张家口市宣化县九年级上学期期末数学试卷

试卷更新日期：2017-03-27 类型：期末考试

进入出卷网下载

一、选择题

1. 下列平面图形中，既是轴对称图形，又是中心对称图形的是（）

A、 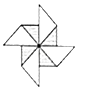B、 C、 D、

查看试题解析
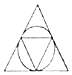2. 一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下列函数解析式：h=﹣3（t﹣2）²+5，则小球距离地面的最大高度是（）

A、2米 B、3米 C、5米 D、6米

查看试题解析
3. 将一元二次方程3x²﹣5=4x化为一般形式后，二次项系数和一次项系数分别是（）

A、﹣3，4 B、3，﹣4 C、﹣3，﹣4 D、3，4

查看试题解析
4. 下列事件中，属于必然事件的是（）

A、任意画一个三角形，其内角和为360° B、打开电视机，正在播放里约奥运会的比赛项目 C、400人中至少有两个人的生日在同一天 D、经过交通信号灯的路口，遇到绿灯

查看试题解析
5. 关于x的一元二次方程x²+4x﹣2k=0有两个实数根，则实数k的取值范围是（）

A、k≥﹣2 B、k≤﹣2 C、k＞﹣2 D、k=﹣2

查看试题解析
6. 下列命题中，属于真命题的是（）

A、圆周角等于圆心角的一半 B、在同一圆中，等弧所对的圆周角相等 C、平分弦的直线垂直于弦 D、过弦的中点的直线必经过圆心

查看试题解析
7. 某品牌LED电视机经过连续两次降价，每台售价由原来的4000元降到了2980元，设平均每次降价的百分率为x，则下列方程中正确的是（）

A、4000（1+x）²=2980 B、2980（1+x）²=4000 C、2980（1﹣x）²=4000 D、4000（1﹣x）²=2980

查看试题解析
8. 如图，AB是⊙O的直径，CD是⊙O的弦，∠ABD=62°，则∠DCB的度数为（）

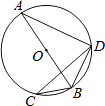A、28° B、30° C、59° D、62°

查看试题解析
9. 在一个不透明的盒子中装有12个红球，若干个篮球，它们除颜色不同外，其余均相同，若从中随机摸出一个球为红球的概率是 $\frac{4}{7}$ ，则篮球的个数为（）

A、4 B、6 C、8 D、9

查看试题解析
10. 如图，将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置，旋转角为30°，则C点运动到C′点的路径长为（）

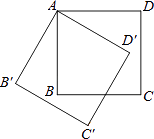A、 $\frac{2}{3}$ πcm B、 $\frac{2 \sqrt{2}}{3}$ πm C、 $\frac{2 \sqrt{3}}{3}$ cm D、 $\frac{2 \sqrt{5}}{3}$ cm

查看试题解析
11. 已知⊙O的面积为4π，则其内接正方形的面积为（）

A、2 B、4 C、8 D、16

查看试题解析
12. 已知二次函数y=x²﹣4x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x²﹣4x+m=0的两个实数根是（）

A、x₁=1，x₂=﹣1 B、x₁=﹣1，x₂=2 C、x₁=﹣1，x₂=0 D、x₁=1，x₂=3

查看试题解析
13. 如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则 $\frac{O C}{C D}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
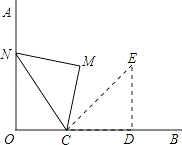14. 如图，在⊙O中，直径AB垂直于弦CD，垂足为P，若PA=4，PB=12，则CP的长为（）

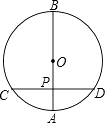A、2 $\sqrt{3}$ B、4 C、8 D、4 $\sqrt{3}$

查看试题解析
15. 已知点（﹣3，y₃），（﹣2，y₁），（﹣1，y₂）在函数y=x²+1的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₃＞y₁＞y₂ C、y₃＞y₂＞y₁ D、y₂＞y₁＞y₃

查看试题解析
16. 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是（）

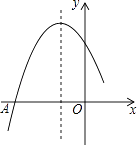A、b²＜4ac B、2a+b=0 C、a+b+c＞0 D、若点B（ $\frac{5}{2}$ ，y₁）、C（ $\frac{1}{2}$ ，y₂）为函数图象上的两点，则y₁＜y₂

查看试题解析

二、填空题

17. 给出一种运算，对于函数y=xⁿ ，规定y′=nxⁿ^﹣²﹣1，若函数y=x⁵ ，则有y′=5x³﹣1．已知函数y=x⁴ ，则方程y′=3x的解的和为．

查看试题解析
18. 已知二次函数y=x²+2mx+2，当x＞2时，y的值随x值的增大而增大，则实数m的取值范围是．

查看试题解析
19. 如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为．

查看试题解析
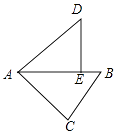20. 如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y= $\frac{1}{2}$ x²+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是．

查看试题解析

三、解答题

21. 解方程：

(1)、2x²﹣7x+3=0

(2)、x（x﹣2）=x．

查看试题解析
22. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2}$ ， $\frac{1}{4}$ ，1的卡片，乙同学手中藏有三张分别标有1，3，2的卡片，卡片外形相同．现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为a，b．

(1)、请你用树形图或列表法列出所有可能的结果．

(2)、现制定这样一个游戏规则：若所选出的a，b能使得ax²+bx+1=0有两个不相等的实数根，则称甲获胜；否则称乙获胜．请问这样的游戏规则公平吗？请你用概率知识解释．

查看试题解析
23.
△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：

(1)、画出△ABC关于原点O的中心对称图形△A₁B₁C₁；

(2)、画出将△ABC绕点A逆时针旋转90°得到△AB₂C₂ ，

(3)、△A₁B₁C₁中顶点A₁坐标为．

查看试题解析
24. 如图，已知△ABC是等边三角形，以AC为直径的⊙O分别交AB，BC于点D，E，点F在AB的延长线上，2∠BCF=∠BAC．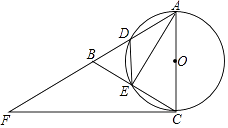

(1)、求∠ADE的度数．

(2)、求证：直线CF是⊙O的切线．

查看试题解析
25. 已知二次函数y=mx²﹣5mx+1（m为常数，m＞0），设该函数的图象与y轴交于点A，该图象上的一点B与点A关于该函数图象的对称轴对称．

(1)、求点A，B的坐标；

(2)、点O为坐标原点，点M为该函数图象的对称轴上一动点，求当M运动到何处时，△MAO的周长最小．

查看试题解析
26. 问题提出
平面内不在同一条直线上的三点确定一个面，那么平面内的四点（任意三点均不在同一直线上），能否在同一个面上呢？
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O．

(1)、当C、D在线段AB的同侧时．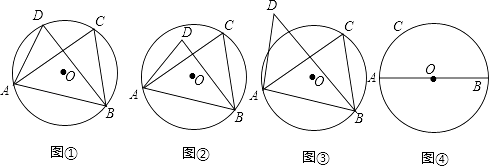
如图①，若点D在⊙O上，此时有∠ACB=∠ADB，理由是．
如图②，若点D在⊙O内，此时有∠ACB∠ADB；
如图③，若点D在⊙O外，此时有∠ACB∠ADB（填“=”、“＞”、“＜”）
由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件：．
类比学习

(2)、仿照上面的探究思路，请探究：当C、D在线段AB的异侧时的情形．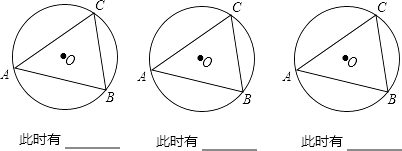
由上面的探究，请用文字语言直接写出A、B、C、D四点在同一个圆上的条件：．
拓展延伸

(3)、如何过圆上一点，仅用没有刻度的直尺，作出已知直径的垂线？
已知：如图，AB是⊙O的直径，点C在⊙O上，求作：CN⊥AB
作法：①连接CA、CB
②在CB上任取异于B、C的一点D，连接DA，DB；
③DA与CB相交于E点，延长AC、BD，交于F点；
④连接F、E并延长，交直径AB与M；
⑤连接D、M并延长，交⊙O于N，连接CN，则CN⊥AB．
请安上述作法在图④中作图，并说明CN⊥AB的理由．（提示：可以利用（2）中的结论）

查看试题解析