2016-2017学年广东省深圳市罗湖区九年级上学期期末数学试卷
试卷更新日期：2017-03-27 类型：期末考试
一、选择题：
-
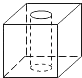
1. 一元二次方程x2﹣1=0的根为（ ）A、x=1 B、x=﹣1 C、x1=1，x2=﹣1 D、x1=0，x2=12. 在Rt△ABC中，∠C=90°，AC=3，BC=4，那么cosB的值是（ ）A、 B、 C、 D、3. 有一个铁制零件（正方体中间挖去一个圆柱形孔）如图放置，它的左视图是（ ）
A、
B、
C、
D、
4. 下列命题正确的是（ ）A、有一组邻边相等的四边形是菱形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的平行四边形是正方形 D、对角线相等且互相垂直的四边形是正方形5. 如图，小明从路灯下A处向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是（ ）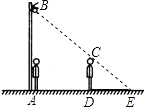
A、4米 B、5.6米 C、2.2米 D、12.5米6. 已知二次函数y=ax2的图象如图所示，则关于x的一元二次方程x2+x+a﹣1=0的根的存在情况是（ ）
A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定7. 某公司今年销售一种产品，一月份获得利润10万元，由于产品畅销，利润逐月增加，一季度共获利36.4万元，已知2月份和3月份利润的月增长率相同．设2，3月份利润的月增长率为x，那么x满足的方程为（ ）A、10（1+x）2=36.4 B、10+10（1+x）2=36.4 C、10+10（1+x）+10（1+2x）=36.4 D、10+10（1+x）+10（1+x）2=36.48. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根，则该三角形的周长可以是（ ）A、5 B、7 C、5或7 D、109. 如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E的度数是（ ）
A、45° B、30° C、20° D、15°10. 如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A、②④ B、①④ C、②③ D、①③11. 如图，在菱形ABCD中，∠BAD=60°，点M是AB的中点，P是对角线AC上的一个动点，若PM+PB的最小值是9，则AB的长是（ ）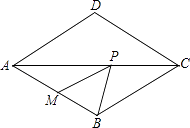
A、6 B、3 C、9 D、4.512. 如图，已知直线y= x与双曲线y= （k＞0）交于A、B两点，点B的坐标为（﹣4，﹣2），C为双曲线y= （k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（ ）
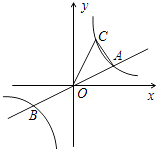A、（2，4） B、（1，8） C、（2，4）或（1，8） D、（2，4）或（8，1）二、填空题：
-
13. 某口袋中有红色、黄色、蓝色玻璃球共72个，小明通过多次摸球试验后，发现摸到红球、黄球、蓝球的频率为35%、25%和40%，估计口袋中黄色玻璃球有个．14. 若关于x的一元二次方程（m﹣1）x2+5x+m2﹣3m+2=0的一个根是0，则m的值是 ．15.
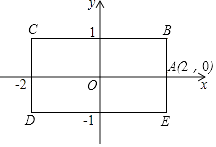
如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2016次相遇地点的坐标是 ．
16. 如图1，在矩形纸片ABCD中，AB=8 ，AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG= ．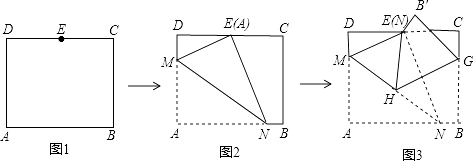
三、解答题：
-
17. 解方程：(1)、x2+3x﹣2=0；(2)、（x﹣3）（x+1）=x﹣3．18. 小明参加某网店的“翻牌抽奖”活动，如图，4张牌分别对应价值5，10，15，20（单位：元）的4件奖品．
(1)、如果随机翻1张牌，那么抽中20元奖品的概率为 ．(2)、如果随机翻2张牌，且第一次翻过的牌不再参加下次翻牌，请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少？19. 如图．矩形ABCD的对角线相交于点O．DE∥AC，CE∥BD．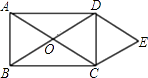
(1)、求证：四边形OCED是菱形；(2)、若∠ACB=30°，菱形OCED的面积为8 ，求AC的长．20.如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底部G点为BC的中点，求矮建筑物的高CD．
21. 某景区商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个；第二周若按每个10元的价格销售仍可售出200个，但商店为了提高销售量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出．(1)、如果这批旅游纪念品共获利1050元，那么第二周每个旅游纪念品的销售价格为多少元？(2)、第二周每个旅游纪念品的销售价格为多少时，这批旅游纪念品利润最大？最大利润是多少？22. 如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．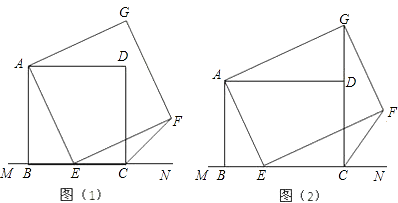
(1)、连接GD，求证：△ADG≌△ABE；(2)、连接FC，观察并猜测∠FCN的度数，并说明理由；(3)、如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．23.如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0， ），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．
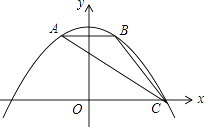(1)、求该抛物线的函数关系表达式．(2)、点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．(3)、将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．