2016-2017学年安徽省芜湖市九年级上学期期末数学试卷
试卷更新日期:2017-03-27 类型:期末考试
一、选择题:
-
1. 观察下列“风车”的平面图案:其中是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 用配方法解方程x2+x﹣1=0,配方后所得方程是( )A、(x﹣ )2= B、(x+ )2= C、(x﹣ )2= D、(x+ )2=3. 函数y= 的图象经过点A(1,﹣2),则k的值为( )A、 B、﹣ C、2 D、﹣24. 如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )
A、1个 B、2个 C、3个 D、4个2. 用配方法解方程x2+x﹣1=0,配方后所得方程是( )A、(x﹣ )2= B、(x+ )2= C、(x﹣ )2= D、(x+ )2=3. 函数y= 的图象经过点A(1,﹣2),则k的值为( )A、 B、﹣ C、2 D、﹣24. 如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )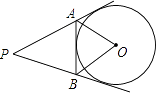 A、50° B、60° C、70° D、80°5. 若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为( )A、 B、 C、 或 D、a+b或a﹣b6. 若非零实数a、b满足4a2+b2=4ab,则 =( )A、2 B、﹣2 C、4 D、﹣47. ⊙O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )A、 B、2 C、 D、38. 如图,正比例函数y1=k1x的图象与反比例函数y2= 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
A、50° B、60° C、70° D、80°5. 若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为( )A、 B、 C、 或 D、a+b或a﹣b6. 若非零实数a、b满足4a2+b2=4ab,则 =( )A、2 B、﹣2 C、4 D、﹣47. ⊙O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )A、 B、2 C、 D、38. 如图,正比例函数y1=k1x的图象与反比例函数y2= 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )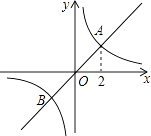 A、x<﹣2或x>2 B、x<﹣2或0<x<2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>29. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是( )
A、x<﹣2或x>2 B、x<﹣2或0<x<2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>29. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是( ) A、3cm2 B、4cm2 C、5cm2 D、6cm211. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、
A、3cm2 B、4cm2 C、5cm2 D、6cm211. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、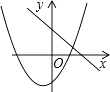 B、
B、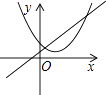 C、
C、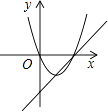 D、
D、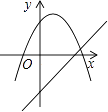 12. 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2 ,BD= ,则AB的长为( )
12. 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2 ,BD= ,则AB的长为( )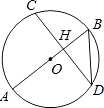 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题:
-
13. 已知一元二次方程x2+4x﹣12=0的两根的平方和= .14. 四条木棒长为1,4,5,8,选其中三条组成三角形的概率是 .15. 若 是反比例函数,则m= .16. P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= .
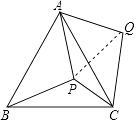 17. 点P(1,a)在反比例函数 的图象上,它关于y轴的对称点在一次函数y=2x+4的图象上,则此反比例函数的解析式为 .18. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为 m.
17. 点P(1,a)在反比例函数 的图象上,它关于y轴的对称点在一次函数y=2x+4的图象上,则此反比例函数的解析式为 .18. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为 m.
三、解答题:
-
19. 解方程:x2﹣2x=2x+1.20. 小明在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 求金色纸边的宽度.
 21. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1),B(1,n)两点.
21. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1),B(1,n)两点.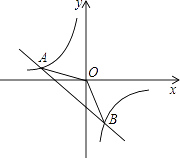 (1)、试确定上述反比例函数和一次函数的表达式;(2)、求△AOB的面积.22. 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)、试确定上述反比例函数和一次函数的表达式;(2)、求△AOB的面积.22. 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).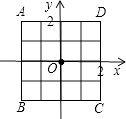 (1)、求P点落在正方形ABCD面上(含正方形内部和边界)的概率.(2)、将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
(1)、求P点落在正方形ABCD面上(含正方形内部和边界)的概率.(2)、将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为 ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
23. 如图,顶点为A( ,1)的抛物线经过坐标原点O,与x轴交于点B.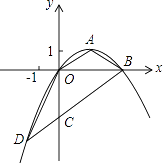 (1)、求抛物线对应的二次函数的表达式;(2)、过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)、在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
(1)、求抛物线对应的二次函数的表达式;(2)、过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)、在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.