湖北省黄冈市武穴市大金镇2017-2018学年八年级下学期数学期末测试卷
试卷更新日期:2018-12-02 类型:期末考试
一、单选题
-
1. 三角形三条边的长有下面四组:①0.3、0.4、0.5;②2、5、6;③1、 . 、④1、4、4.可构成直角三角形的有( )A、1组 B、2组 C、3组 D、4组2. 下面各组数据能判断是直角三角形的是( )A、三边长都为2 B、三边长分别为2,3,2 C、三边长分别为13,12,5 D、三边长分别为4,5,63. 有一对角线长为200cm的长方形黑板,小明测得长为160cm,那么这块黑板的宽为( )A、180cm B、120cm C、160cm D、64cm4. 如图是某地的长方形广场的示意图,如果小红要从点A走到点C,那么他至少要走( )
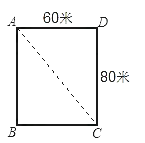 A、90米 B、100米 C、120米 D、140米5. 在△ABC中,∠A=90°,∠A,∠B,∠C的对边长分别为a、b、c,则下列结论错误的是( )A、a2+b2=c2 B、b2+c2=a2 C、a2-b2=c2 D、a2-c2=b26. 在一块平地上,张大爷家屋前9米远处有一颗大树,在一次强风中,这课大树从离地面6米处折断倒下,量得倒下部分的长是10米,大树倒下时能砸到张大爷的房子吗?( )
A、90米 B、100米 C、120米 D、140米5. 在△ABC中,∠A=90°,∠A,∠B,∠C的对边长分别为a、b、c,则下列结论错误的是( )A、a2+b2=c2 B、b2+c2=a2 C、a2-b2=c2 D、a2-c2=b26. 在一块平地上,张大爷家屋前9米远处有一颗大树,在一次强风中,这课大树从离地面6米处折断倒下,量得倒下部分的长是10米,大树倒下时能砸到张大爷的房子吗?( ) A、一定不会 B、可能会 C、一定会 D、以上答案都不对7. 若一直角三角形两边长分别为12和5,则第三边长为( )A、13 B、13或 C、13或15 D、158. 在 ABC,如果AC2-AB2=BC2 , 那么( )A、 A= B、 B= C、 C= D、不能确定9. △ABC的三边长分别为a,b,c,下列条件:
A、一定不会 B、可能会 C、一定会 D、以上答案都不对7. 若一直角三角形两边长分别为12和5,则第三边长为( )A、13 B、13或 C、13或15 D、158. 在 ABC,如果AC2-AB2=BC2 , 那么( )A、 A= B、 B= C、 C= D、不能确定9. △ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;
②∠A∶∠B∶∠C=3∶4∶5;
③a2=(b+c)(b-c);
④a∶b∶c=5∶12∶13,
其中能判定△ABC是直角三角形的有( )
A、1个 B、2个 C、3个 D、4个10. 下列各组长度的线段能构成直角三角形的一组是( )A、30,40,50 B、7,12,13 C、5,9,12 D、3,4,6二、填空题
-
11. 下列各组数:①1、2、3;②6、8、10;③0.3、0.4、0.5;④9、40、41;其中是勾股数的有 (填序号)
12. 在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .13. 一个直角三角形的两条直角边的长分别为5cm和12cm,则斜边长为cm。14. 一个三角形的三边BC,AC,AB有如下关系:BC2=AC2+AB2 , 则Rt△ABC中的直角是 .
15. 学校有一块长方形花圃,有极少数人为了避免拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了步路(假设2步为1米),却踩伤了花草.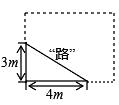
三、解答题
-
16. 在△ABC中,AB=AC,D是BC延长线上的点,求证:
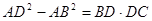 . 17. 当a、b、c为何值时,代数式 有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积.18. 已知a,b,c为正数,满足如下两个条件:
. 17. 当a、b、c为何值时,代数式 有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积.18. 已知a,b,c为正数,满足如下两个条件:a+b+c=32 ①
②
是否存在以 , , 为三边长的三角形?如果存在,求出三角形的最大内角.
19. 一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?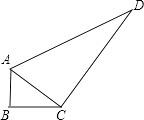 20. 如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?
20. 如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?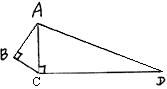
四、综合题
-
21. 已知:如图Rt△ABC中,∠C=90°,AC= +1,BC= ﹣1.求:
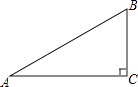 (1)、Rt△ABC的面积;(2)、斜边AB的长.22. 如图所示,在 中, , ,在 中, 为 边上的高, , 的面积 .
(1)、Rt△ABC的面积;(2)、斜边AB的长.22. 如图所示,在 中, , ,在 中, 为 边上的高, , 的面积 .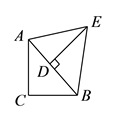 (1)、求出 边的长.(2)、你能求出 的度数吗?请试一试.
(1)、求出 边的长.(2)、你能求出 的度数吗?请试一试.
23. 如图,AB∥CD,CE平分∠ACD交AB于点E.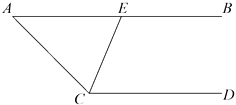 (1)、求证:△ACE是等腰三角形.
(1)、求证:△ACE是等腰三角形.
(2)、若AC=13,CE=10,求△ACE的面积.
