四川省巴中市南江县 2018—2019学年上学期八年级数学期末模拟测试卷
试卷更新日期:2018-11-30 类型:期末考试
一、单选题
-
1. 在△ABC和△A'B'C'中,已知∠A=∠A′,AB=A′B′,则添加下列条件后不能判定两个三角形全等的是( )
A、AC=A′C′ B、BC=B′C′ C、∠B=∠B′ D、∠C=∠C′2. 不论x,y为任何实数,x2+y2﹣4x﹣2y+8的值总是( )A、正数 B、负数 C、非负数 D、非正数3. 下列各组数中,是勾股数的一组为A、3,4,25 B、6,8,10 C、5,12,17 D、8,7,64. 下列说法中正确的是( )A、原命题是真命题,则它的逆命题不一定是真命题 B、原命题是真命题,则它的逆命题不是命题 C、每个定理都有逆定理 D、只有真命题才有逆命题5. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F.S△ABC=7,DE=2,AB=4,则AC长是( )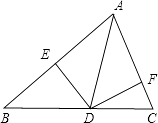 A、4 B、3 C、6 D、56. 已知:2a=3,2b=6,2c=12,则a、b、c的关系是( )A、a+b>2c B、2b<a+c C、2b=a+c D、2b>a+c7. 下列语句不是命题的是( )A、两点之间线段最短 B、互补的两个角之和是180° C、画两条相交直线 D、相等的两个角是对顶角8. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:
A、4 B、3 C、6 D、56. 已知:2a=3,2b=6,2c=12,则a、b、c的关系是( )A、a+b>2c B、2b<a+c C、2b=a+c D、2b>a+c7. 下列语句不是命题的是( )A、两点之间线段最短 B、互补的两个角之和是180° C、画两条相交直线 D、相等的两个角是对顶角8. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论: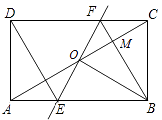
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A、1 B、2 C、3 D、49. 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) A、 = B、AD,AE将∠BAC三等分 C、△ABE≌△ACD D、S△ADH=S△CEG
A、 = B、AD,AE将∠BAC三等分 C、△ABE≌△ACD D、S△ADH=S△CEG二、填空题
-
10. ﹣4是的立方根.11. 分解因式: = .12. 计算: = .13. 计算:(﹣2)4×( )5= .14. 如图,已知 , , 要使≌ , 可补充的条件是 (写出一个即可).
 15. 填空:在﹣0.8,1, ,0,8.9,﹣6,﹣1.1212212221…,在这些数中,
15. 填空:在﹣0.8,1, ,0,8.9,﹣6,﹣1.1212212221…,在这些数中,正数有 . 整数有 . 无理数有 .
16. 已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4cm,则△DEF中的EF边等于 cm.17. 已知等腰 中, , 是 边上一点,连结 .若 和 都是等腰三角形,则 的度数为 .18. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有.(填序号) 19. 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子 .
19. 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子 .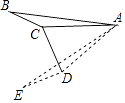
三、计算题
-
20. ①计算:(-1)2+ - -︱-5︱
②用适当的方法解方程:x2=2x+35.
21. 计算:(1)、(2x)3•y3÷16xy2(2)、x2﹣(x+3)(x﹣3)(3)、简便计算:201×199.22. 给出三个多项式:a2+3ab﹣2b2 , b2﹣3ab,ab+6b2 , 任请选择两个多项式进行加法运算,并把结果分解因式.四、解答题
-
23. 阅读以下作图过程:
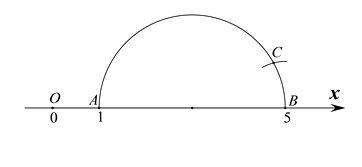
第一步:在数轴上,点O表示数0,点A表示数1,点B表示数5,以AB为直径作半圆(如图);
第二步:以B点为圆心,1为半径作弧交半圆于点C(如图);
第三步:以A点为圆心,AC为半径作弧交数轴的正半轴于点M.
请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M表示的数
 24. 如图,在△ABC中,∠A=90 ° ,BD是角平分线,DE⊥BC于点E,若AD=3,BC=4,求△BDC的面积.
24. 如图,在△ABC中,∠A=90 ° ,BD是角平分线,DE⊥BC于点E,若AD=3,BC=4,求△BDC的面积. 25. 某校为积极开展人防教育,抽取了部分八年级的学生举行人防知识竞赛,并将竞赛成绩整理后作出如下的统计图。已知从左至右第一、二组的频率和是0.12,第二、三、四组的频数比是4:17:15,成绩不小于100分的同学占96%。结合统计图回答下列问题:
25. 某校为积极开展人防教育,抽取了部分八年级的学生举行人防知识竞赛,并将竞赛成绩整理后作出如下的统计图。已知从左至右第一、二组的频率和是0.12,第二、三、四组的频数比是4:17:15,成绩不小于100分的同学占96%。结合统计图回答下列问题:
(1)从左至右第一组的频率是多少?共有多少人参加了这次人防知识竞赛?
(2)成绩不小于130分的为优秀,若将原统计图改成扇形统计图,则优秀部分对应的圆心角应画成几度角?
(3)如果这次竞赛成绩的中位数是120分,那么成绩为120分的学生至少有多少人? 26. 如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
26. 如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE. (1)、求证:BD=AE;(2)、若∠BAC=70°,求∠BPE的度数.
(1)、求证:BD=AE;(2)、若∠BAC=70°,求∠BPE的度数.五、综合题
-
27. 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
 (1)、∠C=∠E;(2)、AB=AD.28. 综合题
(1)、∠C=∠E;(2)、AB=AD.28. 综合题
(1)、如图1,在△ABC中∠A=60 º,BD、CE均为△ABC的角平分线且相交于点O.①填空:∠BOC=度;
②求证:BC=BE+CD.(写出求证过程)
 (2)、如图2,在△ABC中,AB=AC=m,BC=n, CE平分∠ACB.
(2)、如图2,在△ABC中,AB=AC=m,BC=n, CE平分∠ACB.①若△ABC的面积为S,在线段CE上找一点M,在线段AC上找一点N,使得AM+MN的值最小,则AM+MN的最小值是 . (直接写出答案);
②若∠A=20°,则△BCE的周长等于 . (直接写出答案).
 29. 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
29. 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.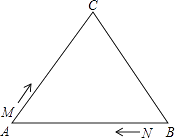 (1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边三角形△AMN?(3)、当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
(1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边三角形△AMN?(3)、当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.