山东省2018届高三天成大联考文数第二次考试试卷

试卷更新日期：2018-11-29 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合 $A = {x | 3^{x} < \frac{1}{3}}$ ， $B = {x | | x | = - x}$ ，则 $A \cap^{} B =$ （）

A、 $(- 1 ， 0)$ B、 $(2 ， + \infty)$ C、 $(- \infty ， - 1)$ D、 $(- \infty ， 0]$

查看试题解析
2. 复数 $z = (i - 3) i$ ( $i$ 为虚数单位)在复平面内所对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. “ $\forall x \in R$ ， $x^{3} - 3 x > 0$ ”的否定为（）

A、 $\exists x \in R$ ， $x^{3} - 3 x \leq 0$ B、 $\forall x \in R$ ， $x^{3} - 3 x < 0$ C、 $\forall x \in R$ ， $x^{3} - 3 x \leq 0$ D、 $\exists x \in R$ ， $x^{3} - 3 x > 0$

查看试题解析
4. 曲线 $f (x) = 2 x - e^{x}$ 在点 $(0 ， f (0))$ 处的切线方程是（）

A、 $x + y + 1 = 0$ B、 $x - y + 1 = 0$ C、 $x + y - 1 = 0$ D、 $x - y - 1 = 0$

查看试题解析
5. 已知甲、乙、丙三人中，一人是公务员，一人是医生，一人是教师.若丙的年龄比教师的年龄大；甲的年龄和医生的年龄不同；医生的年龄比乙的年龄小，则下列判断正确的是（）

A、甲是公务员，乙是教师，丙是医生 B、甲是教师，乙是公务员，丙是医生 C、甲是教师，乙是医生，丙是公务员 D、甲是医生，乙是教师，丙是公务员

查看试题解析
6. 若执行如图所示的程序框图，则输出的i的值是（）

A、5 B、7 C、9 D、11

查看试题解析
7. 若 $a > 0$ ， $b > 0$ 且 $2 a + b = 4$ ，则 $\frac{1}{a b}$ 的最小值为（）

A、2 B、 $\frac{1}{2}$ C、4 D、 $\frac{1}{4}$

查看试题解析
8. 已知抛物线 $C ： y^{2} = 4 x$ ，若过点 $P (- 2 ， 0)$ 作直线 $l$ 与抛物线 $C$ 交 $A$ ， $B$ 两个不同点，且直线 $l$ 的斜率为 $k$ ，则 $k$ 的取值范围是（）

A、 $(- \frac{\sqrt{2}}{2} ， 0) \cup^{} (0 ， \frac{\sqrt{2}}{2})$ B、 $[- \frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2}]$ C、 $(- \frac{\sqrt{3}}{2} ， \frac{\sqrt{3}}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， 0) \cup^{} (0 ， \frac{\sqrt{3}}{2})$

查看试题解析
9. 《九章算术》是我国古代的数学名著，书中有如下间题：“今有甲、乙、丙、丁、戊五人分五饯，令上二人所得与下三人等，且五人所得钱按顺序等次差，问各得几何？”其意思为“甲、乙、丙、丁、戊五人分五钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列，问五人各得多少钱(钱：古代一种重量单位)？”这个问题中丙所得为（）

A、 $\frac{7}{6}$ 钱 B、 $\frac{4}{3}$ 钱 C、1钱 D、 $\frac{5}{6}$ 钱

查看试题解析
10. 已知不等式组 ${\begin{matrix} x - 2 y \geq 0 ， \\ x + 2 y \leq 4 ， \\ y \geq 0 ， \\ x + y \leq m \end{matrix}$ 表示的平面区域为 $M$ .若平面区域 $M$ 内的整点(横、纵坐标都是整数的点) 恰有3个，则整数 $m$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
11. 函数 $f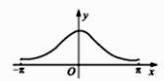 (x) = x e^{cos x} (x \in [- π ， π])$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
12. 设函数 $f (x) = x^{2} - 2 e x - \frac{ln x}{x} + a$ (其中 $e$ 为自然对数的底数，若函数 $f (x)$ 至少存在一个零点，则实数a的取值范围是（）

A、 $(0 ， e^{2} - \frac{1}{e}]$ B、 $(0 ， e^{2} + \frac{1}{e}]$ C、 $[e^{2} - \frac{1}{e} ， + \infty)$ D、 $(- \infty ， e^{2} + \frac{1}{e}]$

查看试题解析

二、填空题

13. 已知向量 $a = (- k ， k + 2)$ ， $b = (2 ， - 3)$ ，若 $a / / (a + 2 b)$ ，则实数 $k =$ ．

查看试题解析
14. 已知圆 $C$ 经过坐标原点和点 $(4 ， 0)$ ，若直线 $y = 1$ 与圆 $C$ 相切，则圆 $C$ 的方程是．

查看试题解析
15. 若在各项都为正数的等比数列 ${a_{n}}$ 中， $a_{1} = 2$ ， $a_{9} = a_{3}^{3}$ ，则 $a_{2018} =$ ．

查看试题解析
16. 若 $F_{1}$ ， $F_{2}$ 分別是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ $(a > 0 ， b > 0)$ 的左、右焦点， $O$ 为坐标原点，点 $P$ 在双曲线的左支上，点 $M$ 在直线 $x = \frac{a^{2}}{c} (c = \sqrt{a^{2} + b^{2}})$ 上，且满足 $\overset{⇀}{F_{1} O} = \overset{⇀}{P M}$ ， $\overset{⇀}{O P} = λ (\frac{\overset{⇀}{O F_{1}}}{| \overset{⇀}{O F_{1}} |} + \frac{\overset{⇀}{O M}}{| \overset{⇀}{O M} |}) (λ > 0)$ ，则该双曲线的离心率为．

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，且 ${sin}^{2} B + {sin}^{2} C = {sin}^{2} A + sin B sin C$ .

(1)、求角 $A$ 的大小；

(2)、若 $a = 6$ ，求 $b + c$ 的最大值.

查看试题解析
18. 已知等差数列 ${a_{n}}$ 的公差为 $d$ ，且关于 $x$ 的不等式 $a_{1} x^{2} - d x - 3 < 0$ 的解集为 $(- 1 ， 3)$ ，

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = 2^{a_{n}} + 2 a_{n}$ ，求数列 ${b_{n}}$ 前 $n$ 项和 $S_{n}$ .

查看试题解析
19. 已知函数 $f (x) = 2 sin 8 x cos 4 x sin (4 x + \frac{π}{6}) - cos 8 x sin 4 x (\sqrt{3} sin 4 x + cos 4 x)$ .

(1)、求函数 $f (x)$ 图象的对称中心；

(2)、求函数 $f (x)$ 的单调递减区间.

查看试题解析
20. 已知点 $A (a ， 0)$ ， $B (0 ， b)$ 分别是椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的长轴端点、短轴端点， $O$ 为坐标原点，若 $\overset{⇀}{A B} \cdot \overset{⇀}{A O} = 16$ ， $| \overset{⇀}{O A} + \overset{⇀}{O B} | = 2 \sqrt{5}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、如果斜率为 $k_{1}$ 的直线 $l$ 交椭圆 $C$ 于不同的两点 $E ， F$ (都不同于点 $A ， B$ )，线段 $E F$ 的中点为 $M$ ，设线段 $O M$ 的垂线 $l^{'}$ 的斜率为 $k_{2}$ ，试探求 $k_{1}$ 与 $k_{2}$ 之间的数量关系.

查看试题解析
21. 已知函数 $f (x) = ln x$ ， $g (x) = \frac{x - a}{2 x} (a \in R)$ .

(1)、讨论函数 $g (x)$ 的单调性；

(2)、若 $a = 1$ ， $f (x) \geq m g (x)$ 对任意 $x \in [1 ， + \infty)$ 恒成立，求实数 $m$ 的取值范围.

查看试题解析
22. 已知在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程是 ${\begin{matrix} x = t \\ y = 2 t + 6 \end{matrix}$ ( $t$ 是参数)，以原点 $O$ 为极点， $x$ 轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ = 2 \sqrt{2} cos θ$ .

(1)、求直线 $l$ 与曲线 $C$ 的普通方程；

(2)、设 $M (x ， y)$ 为曲线 $C$ 上任意一点，求 $x + y$ 的取值范围.

查看试题解析
23. 已知函数 $f (x) = | x - 5 | + | x + 4 |$

(1)、求不等式 $f (x) \geq 12$ 的解集；

(2)、若 $f (x) - 2^{1 - 3 a} - 1 \geq 0$ 对 $\forall x \in R$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析