湖南省邵阳市2019年数学中考模拟试卷
试卷更新日期:2018-11-28 类型:中考模拟
一、选择题
-
1. 在﹣6,0,2.5,|﹣3|这四个数中,最大的数是( )A、﹣6 B、0 C、2.5 D、|﹣3|2. 长城总长约6700010米,用科学记数法表示是(保留两个有效数字)( )
A、67×105米 B、6.7×106米 C、6.7×105米 D、0.67×107米3. 马小虎在学习有理数的运算时,做了如下6道填空题:①(﹣5)+5=0;②﹣5﹣(﹣3)=﹣8;③(﹣3)×(﹣4)=12;④ =1;⑤ ;⑥(﹣4)3=﹣64.你认为他做对了( )
A、6题 B、5题 C、4题 D、3题4. 共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A、1000(1+x)2=1000+440 B、1000(1+x)2=440 C、440(1+x)2=1000 D、1000(1+2x)=1000+4405. 平面直角坐标系中,点(﹣2,4)关于x轴的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 中南商场对上周女装的销售情况进行了统计,销售情况如表:颜色
黄色
绿色
白色
紫色
红色
数量(件)
100
180
220
80
550
经理决定本周进女装时多进一些红色的,可用来解释这一现象的统计知识是( )
A、平均数 B、中位数 C、众数 D、方差7. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、 B、
B、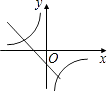 C、
C、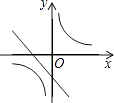 D、
D、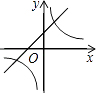 8.
8.如图是几个小正方体组成的一个几何体,这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 9. 小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( )
9. 小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( ) A、14分钟 B、17分钟 C、18分钟 D、20分钟10. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A、14分钟 B、17分钟 C、18分钟 D、20分钟10. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )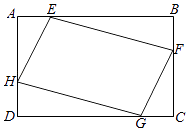 A、5 B、10 C、10 D、15
A、5 B、10 C、10 D、15二、填空题
-
11. 若关于x的方程x2﹣6x+c=0有两个相等的实数根,则c的值为 .12. 现有古代数学问题:“今有牛五羊二值金八两;牛二羊五值金六两,则一牛一羊值金两.
13. 按照如图所示的操作步骤,若输入的x值为-3,则输出的y值为;若依次 输入5个连续的自然数,输出的y的平均数的倒数是50,则所输入的最小的自然数是 . 14. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行13500步与小刚步行9000步消耗的能量相同,若每消耗1千卡能量小琼行走的步数比小刚多15步,求小刚每消耗1千卡能量需要行走步.
14. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行13500步与小刚步行9000步消耗的能量相同,若每消耗1千卡能量小琼行走的步数比小刚多15步,求小刚每消耗1千卡能量需要行走步.
15. 如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,测得MN=39m,则A,B两点间的距离是 m. 16. 如图,四边形ABCD内接于⊙O,若∠B=130°,OA=1,则 的长为 .
16. 如图,四边形ABCD内接于⊙O,若∠B=130°,OA=1,则 的长为 . 17. 如图,等边三角形ABC的边长为9cm, ,连接DE,将 绕点D逆时针旋转,得到 ,连接CF,则 =cm.
17. 如图,等边三角形ABC的边长为9cm, ,连接DE,将 绕点D逆时针旋转,得到 ,连接CF,则 =cm. 18. 如图,点A、B在双曲线y= (x<0)上,连接OA、AB,以OA、AB为边作▱OABC.若点C恰落在双曲线y= (x>0)上,此时▱OABC的面积为 .
18. 如图,点A、B在双曲线y= (x<0)上,连接OA、AB,以OA、AB为边作▱OABC.若点C恰落在双曲线y= (x>0)上,此时▱OABC的面积为 .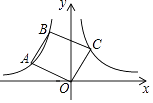
三、解答题
-
19. 计算题(1)、计算:( ﹣π)0﹣6tan30°+( )﹣2+|1﹣ |.(2)、解不等式组 ,并写出它的所有整数解.20. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表.
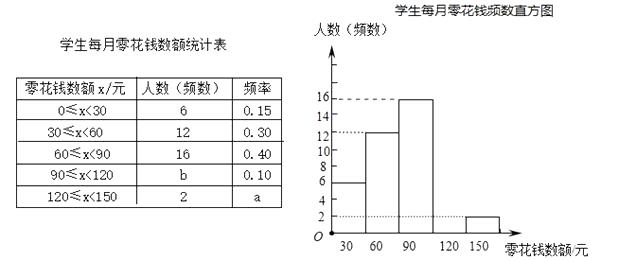
请根据以上图表,解答下列问题:
(1)、这次被调查的人数共有人,a=;
(2)、计算并补全频数分布直方图;
(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.
21. 小明骑自行车从家去学校,途经装有红、绿灯的三个路口.假设他在每个路口遇到红灯和绿灯的概率均为 ,则小明经过这三个路口时,恰有一次遇到红灯的概率是多少?请用树状图的方法加以说明.22. 先化简,再求值:(a﹣2﹣ )÷ ,其中a=(3﹣π)0+( )﹣1 .23. 如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数. ≈1.7, ≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)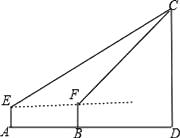 24. 某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.(1)、求购买1个排球、1个篮球的费用分别是多少元?(2)、若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
24. 某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.(1)、求购买1个排球、1个篮球的费用分别是多少元?(2)、若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?四、综合题
-
25.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB.
 (1)、求证:CE⊥AB;(2)、求证:PC是⊙O的切线;(3)、若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.26.
(1)、求证:CE⊥AB;(2)、求证:PC是⊙O的切线;(3)、若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.26.如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
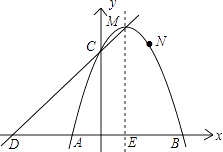 (1)、求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)、若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1)、求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)、若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.