浙教版数学九年级上册《相似三角形》章节提升试卷
试卷更新日期:2018-11-28 类型:单元试卷
一、单选题
-
1. 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20cm,则CQ的长是( )
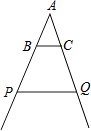 A、8cm B、12cm C、30cm D、50cm2.
A、8cm B、12cm C、30cm D、50cm2.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015 , 到BC的距离记为h2015 . 若h1=1,则h2015的值为( )
 A、 B、 C、1- D、2-3. 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2 ;③tan∠DCF= ;④△ABF的面积为 .其中一定成立的有几个( )
A、 B、 C、1- D、2-3. 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2 ;③tan∠DCF= ;④△ABF的面积为 .其中一定成立的有几个( )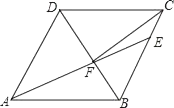 A、1个 B、2个 C、3个 D、4个4. 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
A、1个 B、2个 C、3个 D、4个4. 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )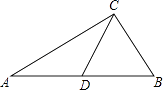 A、 B、2 C、4 ﹣4 D、5. 如图,若果∠1=∠2,那么添加下列任何一个条件:(1) = ,(2) = ,(3)∠B=∠D,(4)∠C=∠AED,其中能判定△ABC∽△ADE的个数为( )
A、 B、2 C、4 ﹣4 D、5. 如图,若果∠1=∠2,那么添加下列任何一个条件:(1) = ,(2) = ,(3)∠B=∠D,(4)∠C=∠AED,其中能判定△ABC∽△ADE的个数为( ) A、1 B、2 C、3 D、46.
A、1 B、2 C、3 D、46.在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2012个正方形的面积为( )
 A、5×2010 B、5×2010 C、5×2012 D、5×40227. 搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( )
A、5×2010 B、5×2010 C、5×2012 D、5×40227. 搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) A、96cm2 B、48cm2 C、24cm2 D、以上都不对8.
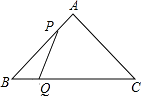
A、96cm2 B、48cm2 C、24cm2 D、以上都不对8.如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
 A、
A、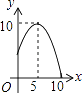 B、
B、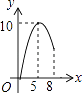 C、
C、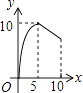 D、
D、 9.
9.如图,在梯形ABCD中,AB∥CD,AB=3CD,对角线AC、BD交于点O,中位线EF与AC、BD分别交于M、N两点,则图中阴影部分的面积是梯形ABCD面积的( )
 A、 B、 C、 D、10. 下列命题正确的有( )个
A、 B、 C、 D、10. 下列命题正确的有( )个①40°角为内角的两个等腰三角形必相似;
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为75°;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一个等腰直角三角形的三边是a、b、c , (a>b=c),那么a2:b2:c2=2:1:1;
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c , 则此△为等腰直角三角形.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为 .
 12. 如图,点P是Rt△ABC斜边AB上的任意一点(A、B两点除外),过点P作一条直线,使截得的三角形与Rt△ABC相似,这样的直线可以作条.
12. 如图,点P是Rt△ABC斜边AB上的任意一点(A、B两点除外),过点P作一条直线,使截得的三角形与Rt△ABC相似,这样的直线可以作条. 13. 若△ABC∽△A′B′C′,∠A=40°,∠C=110°,则∠B′的度数为 .
13. 若△ABC∽△A′B′C′,∠A=40°,∠C=110°,则∠B′的度数为 .
14.如图,在△ABC中,若DE∥BC,= , DE=4cm,则BC的长为 .
 15. 如图,等边 的边 与 轴交于点 ,点 是反比例函数 图像上一点,若 为 边的三等分点时,则等边 的边长为 .
15. 如图,等边 的边 与 轴交于点 ,点 是反比例函数 图像上一点,若 为 边的三等分点时,则等边 的边长为 .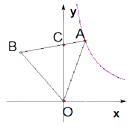 16. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 .下列结论:
16. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 .下列结论:①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8或 ;
④CD2=CE•CA.
其中正确的结论是 (把你认为正确结论的序号都填上)
 17. 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
17. 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 . 18.
18.已知实数a , b , c满足a+b+c=10,且 ,则 的值是
三、解答题
-
19. 如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似?
 20. 如图所示,在矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G.
20. 如图所示,在矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G. (1)、说明点G是线段BC的一个三等分点;(2)、请你依照上面的画法,在原图上画出BC的一个四等分点(保留作图痕迹,不必证明).21.
(1)、说明点G是线段BC的一个三等分点;(2)、请你依照上面的画法,在原图上画出BC的一个四等分点(保留作图痕迹,不必证明).21.如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
 (1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)、如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
22.数学课上,老师要求同学们在扇形纸片OAB上画出一个正方形,使得正方形的四个顶点分别落在扇形半径OA、OB和弧AB上.有一部分同学是这样画的:如图1,先在扇形OAB内画出正方形CDEF,使得C、D在OA上,F在OB上,连结OE并延长交弧AB与G点,过点G,作GJ⊥OA于点J,作GH⊥GJ交OB于点H,再作HI⊥OA于点I.
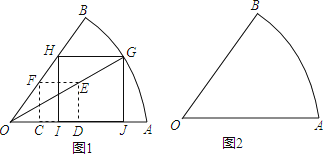
(1)请问他们画出的四边形GHIJ是正方形吗?如果是,请给出你的证明;如果不是,请说明理由;
(2)还有一部分同学用另外一种不同于图1的方法画出的,请你参照图1的画法,在图2上画出这个正方形(保留画图痕迹,不要求证明).
23. 如图1,抛物线 平移后过点A(8,0)和原点,顶点为B,对称轴与 轴相交于点C,与原抛物线相交于点D.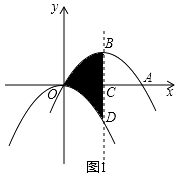
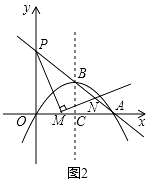
 (1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:
(1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:① 为何值时 为等腰三角形;
②
 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.