2015-2016学年福建省福州市五校联考高一下学期期中数学试卷

试卷更新日期：2017-03-24 类型：期中考试

进入出卷网下载

一、选择题

1. 下列说法正确的是（　　）

A、任何事件的概率总是在（0，1）之间 B、频率是客观存在的，与试验次数无关 C、随着试验次数的增加，频率一般会越来越接近概率 D、概率是随机的，在试验前不能确定

查看试题解析
2. 采用系统抽样方法从学号为1到50的50名学生中选取5名参加测试，则所选5名学生的学号可能是（）

A、1，2，3，4，5 B、5，26，27，38，49 C、2，4，6，8，10 D、5，15，25，35，45

查看试题解析
3. 同时投掷两枚币一次，那么互斥而不对立的两个事件是（）

A、“至少有1个正面朝上”，“都是反面朝上” B、“至少有1个正面朝上”，“至少有1个反面朝上” C、“恰有1个正面朝上”，“恰有2个正面朝上” D、“至少有1个反面朝上”，“都是反面朝上”

查看试题解析
4. 某单位老、中、青人数之比依次为2：3：5．现采用分层抽样方法从中抽出一个容量为n的样本，若样本中中年人人数为12，则此样本的容量n为（）

A、20 B、30 C、40 D、80

查看试题解析
5. 甲、乙、丙三名同学站成一排，甲站在中间的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 执行如图所示的程序框图，若输出的S为4，则输入的x应为（）

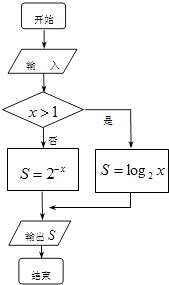A、﹣2 B、16 C、﹣2或8 D、﹣2或16

查看试题解析
7. A是圆上固定的一定点，在圆上其他位置任取一点B，连接A、B两点，它是一条弦，它的长度大于等于半径长度的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{4}$

查看试题解析
8. 某程序框图如图所示，若输出的S=57，则判断框内为（）

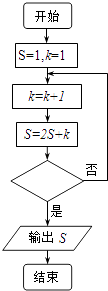A、k＞4？ B、k＞5？ C、k＞6？ D、k＞7？

查看试题解析
9. 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，则时速的众数，中位数的估计值为（）

A、62，62.5 B、65，62 C、65，62.5 D、62.5，62.5

查看试题解析
10. 天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：
907    966    191    925    271    932    812    458    569    683
431    257    393    027    556    488    730    113    537    989
据此估计，这三天中恰有两天下雨的概率近似为（   ）

A、0.35 B、0.25 C、0.20 D、0.15

查看试题解析
11. 如果数据x₁ ， x₂ ， …，x_n的平均数为2，方差为3，则数据3x₁+5，3x₂+5…，3x_n+5的平均数和方差分别为（）

A、11，25 B、11，27 C、8，27 D、11，8

查看试题解析

12. 有三个游戏规则如表，袋子中分别装有形状、大小相同的球，从袋中无放回地取球，

游戏1	游戏2	游戏3
袋中装有3个黑球和2个白球	袋中装有2个黑球和2个白球	袋中装有3个黑球和1个白球
从袋中取出2个球	从袋中取出2个球	从袋中取出2个球
若取出的两个球同色，则甲胜	若取出的两个球同色，则甲胜	若取出的两个球同色，则甲胜
若取出的两个球不同色，则乙胜	若取出的两个球不同色，则乙胜	若取出的两个球不同色，则乙胜

问其中不公平的游戏是（）

A、游戏2 B、游戏3 C、游戏1和游戏2 D、游戏1和游戏3

查看试题解析

二、填空题

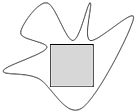
13. 455与299的最大公约数．

查看试题解析
14. 把“二进制”数1011001_（₂_）化为“六进制”数是．

查看试题解析
15. 如图，一不规则区域内，有一边长为1米的正方形，向区域内随机地撒1000颗黄豆，数得落在正方形区域内（含边界）的黄豆数为360颗，以此实验数据1000为依据可以估计出该不规则图形的面积为平方米．（用分数作答）

查看试题解析
16. 在任意三角形ABC内任取一点Q，使S_△_ABQ≥ $\frac{1}{S}$ S_△_ABC的概率为．

查看试题解析

三、解答题：

17. 甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次，记录如下：
甲
88
89
92
90
91
乙
84
88
96
89
93
（Ⅰ）用茎叶图表示这两组数据；
（Ⅱ）现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适？请说明理由．（用样本数据特征来说明．）

查看试题解析
18. 用秦九韶算法计算多项式f（x）=5x⁵+4x⁴+3x³+2x²+x+1，求当x=3时的值．

查看试题解析
19. 如图是计算1+2+ $\frac{1}{2}$ +3+ $\frac{1}{3}$ +…+2010+ $\frac{1}{2010}$ 的值的程序框图，

(1)、图中空白的判断框应填？处理框应填；

(2)、写出与程序框图相对应的程序．

查看试题解析
20. 在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
物体重量（单位g）
1
2
3
4
5
弹簧长度（单位cm）
1.5
3
4
5
6.5
参考公式：
①．样本数据x₁ ， x₂ ， …x_n的标准差
s= $\sqrt{\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]}$ ，其中 $\bar{x}$ 为样本的平均数；
②．线性回归方程系数公式 $\hat{b}$ = $\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{1} - \bar{x})}^{2}}$ = $\frac{\sum_{i = 1}^{n} x_{1} y_{1} - n \cdot \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b}$ $\bar{x}$ ．

(1)、画出散点图；

(2)、利用所给的参考公式，求y对x的回归直线方程；

(3)、预测所挂物体重量为8g时的弹簧长度．

查看试题解析
21. 某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后画出如下部分频率分布直方图．观察图形给出的信息，回答下列问题：

(1)、求第四小组的频率，并补全这个频率分布直方图；

(2)、估计这次考试的及格率（60分及以上为及格）和平均分；

(3)、从成绩是[40，50）和[90，100]的学生中选两人，求他们在同一分数段的概率．

查看试题解析
22. 某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．

(1)、求n的值；

(2)、把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖．求a和b至少有一人上台抽奖的概率．

(3)、抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．

查看试题解析

物体重量（单位g）	1	2	3	4	5
弹簧长度（单位cm）	1.5	3	4	5	6.5

甲	88	89	92	90	91
乙	84	88	96	89	93