山东省2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-27 类型：期中考试
一、选择题
-
1. 如图所示4个汉字中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
2. 三角形的一个外角是锐角，则此三角形的形状是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、无法确定3. 下列长度的三条线段，能组成三角形的是（ ）A、1，1，2 B、2，3，7 C、1，4，6 D、3，4，54. 下列各组数可能是一个三角形的边长的是（ ）A、1，2，4 B、4，5，9 C、4，6，8 D、5，5，115. 等腰三角形有一个角等于70°，则它的底角是（ ）A、70° B、55° C、60° D、70°或55°6. 如图，在△ABC中，∠B，∠C的平分线BE，CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=（ ）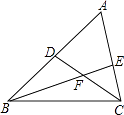
A、118° B、119° C、120° D、121°7. 正六边形的每个内角都是（ ）A、120° B、100° C、80° D、60°8. 等腰三角形的底角为15°，腰长为2a，则腰上的高为（ ）A、 B、2a C、2a-1 D、a9. 如图，在△ABC中，∠C=90°，BD平分∠ABC，交AC于点D；若DC=3，AB=8则△ABD的面积是（ ）
A、8 B、12 C、16 D、2410. 如果等腰三角形两边长是6cm和3cm，那么它的周长是（ ）A、15cm B、12cm C、15cm或12cm D、9cm二、填空题
-
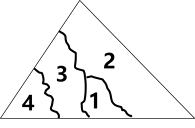
11. 若一个等腰三角形的顶角等于50°，则它的底角等于 ．12. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的带去，就能配一块大小和形状与原来都一样的三角形。
13. 正十二边形的每一个内角是。14. 点（2017，-2018）关于x轴对称的点的坐标为。15. 如图，AC，BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB △DOC，你补充的条件是。
三、解答题
-
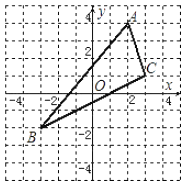
16. 如图所示．请你至少用二种办法，在△ABC中画三条线段．把这个三角形分成面积相等的四部分，并证明其中的一种。
17. 已知：如图，OF是∠AOC和∠BOD的平分线，OA=OC，OB=OD．求证：AB=CD．
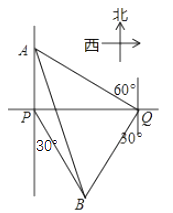
18. 一轮船在P处测得灯塔A在正北方向，灯塔B在南偏东30°方向，轮船向正东航行了900m，到达Q处，测得A位于北偏西60°方向，B位于南偏西30°方向．问：线段BQ与PQ是否相等?请说明理由；
19. 如图，AF=BE，AC∥BD，CE∥DF，
则：
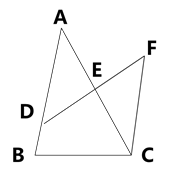
(1)、AC= ， CE=(2)、证明（1）中的结论。20. 如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O．
(1)、求证：BD=CE；(2)、若∠A=80°，求∠BOC的度数．21. 如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB求证：AE=CE．
22. 如图，在△ABC中，∠C=90°，AD平分∠BAC．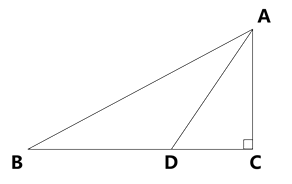
(1)、当∠B=40°时，求∠ADC的度数；(2)、若AB=10cm，CD=4cm，求△ABD的面积
