湖北省武汉市江汉区2018～2019学年七年级上学期数学期中考试试卷

试卷更新日期：2018-11-27 类型：期中考试

进入出卷网下载

一、单选题

1. －2的倒数是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、－2 D、2

查看试题解析
2. 下列式子中，计算结果是5的是（）

A、－2＋|－3| B、|－2－3| C、－2－3 D、|－2|－3

查看试题解析
3. 若x＝－1是关于x的方程2x＋3＝a的解，则a的值为（）

A、－5 B、5 C、1 D、－1

查看试题解析
4. 下列各式中，与2a²b是同类项的是（）

A、abc B、－a²b C、ab² D、2²b²

查看试题解析
5. 第七届世界军人运动会将于2019年在武汉举行，为此武汉将建设军运会历史上首个运动员村，其总建筑面积为558000平方米，数字558000用科学记数法表示为（）

A、0.558×10⁶ B、5.58×10⁴ C、5.58×10⁵ D、55.8×10⁴

查看试题解析
6. 下列各式中，运算正确的是（）

A、3a＋2b＝5ab B、3a²b－3ba²＝0 C、a³＋a²＝a⁵ D、5a²－4a²＝1

查看试题解析
7. 某企业今年1月份产值为x万元，2月份的产值比1月份减少了10%，则2月份的产值是（）

A、(1－10%)x万元 B、(1－10%x)万元 C、(x－10%)万元 D、(1＋10%)x万元

查看试题解析
8. 下列说法正确的是（）

A、－2是单项式 B、 $\frac{2}{x - 2}$ 是多项式 C、3²xy³是六次单项式 D、 $\frac{2 x + 3}{5}$ 的常数项是3

查看试题解析
9. 已知a、b是有理数，满足a＜0＜b，a＋b＞0，则把a、－a、b、－b按照从小到大的顺序排列，正确的是（）

A、－b＜－a＜a＜b B、－b＜a＜－a＜b C、－a＜－b＜a＜b D、a＜－b＜b＜－a

查看试题解析
10. 下列各式运用等式的性质变形，错误的是（）

A、若－a＝－b，则a＝b B、若 $\frac{a}{c} = \frac{b}{c}$ ，则a＝b C、若ac＝bc，则a＝b D、若(m²＋1)a＝(m²＋1)b，则a＝b

查看试题解析

二、填空题

11. 用四舍五入法将3.1416精确到0.01后，得到的近似数是

查看试题解析
12. 如果水位升高3m时水位变化记作＋3m，那么水位下降2m时水位变化记作

查看试题解析
13. 已知x的2倍与10的和等于18，根据题意可列等式为

查看试题解析
14. 在数轴上，点A表示的数为－3，将点A在数轴上移动4个单位长度到达点B，则点B表示的数是

查看试题解析
15. 船在静水中的速度为a千米/时，水流速度为18千米/时，船顺水航行5小时的行程比船逆水航行4小时的行程多千米

查看试题解析
16. 如图，已知四个有理数m、n、p、q在数轴上对应的点分别为M、N、P、Q，且m＋p＝0，则在m、n、p、q四个有理数中，绝对值最小的一个是

查看试题解析
17. 若a－b＝2019，c＋d＝2018，则(b＋c)－(a－d)的值是

查看试题解析
18. 已知(a－3)²＋|b－2|＝0，|m|＝|n|，且mn≠0，则 $\frac{(a + 1) m}{b^{2} n}$ 的值为

查看试题解析
19. 实数a、b在数轴上对应点的位置如图所示，则下列结论：①a－b＞1；②a²＞b²；③ab＞0；④ $\frac{a}{b} > - 1$ ，其中正确结论的序号是。

查看试题解析
20. 九格幻方有如下规律：处于同一横行、同一竖列、同一斜对角线上的三个数的和都相等（如图1）．则图2的九格幻方中的9个数的和为（用含a的式子表示）

查看试题解析

三、解答题

21. 计算：

(1)、23＋(－17)＋6－22

(2)、 $1.25 \times (- 3 \frac{1}{5}) \div (\frac{1}{2} - \frac{1}{3})$

查看试题解析
22. 化简：

(1)、4a²＋3b²＋2ab－4a²－4b²

(2)、5(x－2y)－3(2y－3x)

查看试题解析
23.

(1)、计算： $\frac{7}{3} \div (- \frac{7}{15}) - (- 2) \times [{(- 4)}^{2} + 2] + {(- 2)}^{3}$

(2)、求多项式 $3 a + a b c - (3 a - \frac{1}{3} c^{2}) - \frac{1}{3} c^{2}$ 的值，其中 $a = - \frac{1}{6}$ ，b＝2，c＝－3

查看试题解析
24. 某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的重量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准重量的差值（单位：g）
－5
－2
0
1
3
6
袋数
1
4
3
4
5
3

(1)、计算这批样品的平均重量，判断它比标准重量重还是轻多少？

(2)、若标准重量为450克，则这批样品的总重量是多少？

(3)、若这种食品的合格标准为450±5克，则这批样品的合格率为（直接填写答案）

查看试题解析
25. 某校要将一块长为a米，宽为b米的长方形空地设计成花园，现有如下两种方案供选择.
方案一：如图1，在空地上横、竖各铺一条宽为4米的石子路，其余空地种植花草.
方案二：如图2，在长方形空地中留一个四分之一圆和一个半圆区域种植花草，其余空地铺筑成石子路.

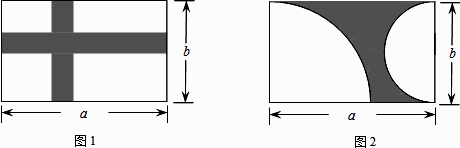(1)、分别表示这两种方案中石子路（图中阴影部分）的面积（若结果中含有π，则保留）

(2)、若a＝30，b＝20，该校希望多种植物美化校园，请通过计算选择其中一种方案（π取3.14）.

查看试题解析
26. 已知A＝2x²＋3xy－2x－1，B＝x²－xy－1

(1)、化简：4A－(2B＋3A)，将结果用含有x、y的式子表示

(2)、若式子4A－(2B＋3A)的值与字母x的取值无关，求 $y^{3} + \frac{7}{125} A - \frac{14}{125} B$ 的值

查看试题解析
27. 观察下面三行数：
①2，－4，8，－16，32，－64……；
②3，－3，9，－15，33，－63……；
③－1，2，﹣4，8，－16，32……；
取每一行的第n个数，依次记为x、y、z．如上图中，当n＝2时，x＝－4，y＝－3，z＝2

(1)、当n＝7时，请直接写出x、y、z的值，并求这三个数中最大的数与最小的数的差

(2)、已知n为偶数，且x、y、z这三个数中最大的数与最小的数的差为384，求n的值；

(3)、若m＝x＋y＋z，则x、y、z这三个数中最大的数与最小的数的差为（用含m的式子表示）

查看试题解析
28. 如图，在数轴上，点A、B表示的数分别是－4、8（A、B两点间的距离用AB表示），点M、N是数轴上两个动点，分别表示数m、n

(1)、AB＝个单位长度；若点M在A、B之间，则|m＋4|＋|m－8|＝

(2)、若|m＋4|＋|m－8|＝20，求m的值

(3)、若点M、点N既满足|m＋4|＋n＝6，也满足|n－8|＋m＝28，则m＝；n＝

查看试题解析

与标准重量的差值（单位：g）	－5	－2	0	1	3	6
袋数	1	4	3	4	5	3