山东省2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2018-11-27 类型:期中考试
一、选择题
-
1. 如图:下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,⊿ABC内接于⊙O,若么∠OAB=28°则∠C的大小为( )
2. 如图,⊿ABC内接于⊙O,若么∠OAB=28°则∠C的大小为( )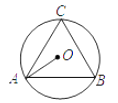 A、56° B、60° C、62° D、28°3. 过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为( )A、3cm B、6cm C、cm D、9cm4. 点P在第二象限内,P到x轴的距离是4,到y轴的距离是5,那么点P关于原点的对称点的坐标是( )
A、56° B、60° C、62° D、28°3. 过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为( )A、3cm B、6cm C、cm D、9cm4. 点P在第二象限内,P到x轴的距离是4,到y轴的距离是5,那么点P关于原点的对称点的坐标是( )
A、(-5,4) B、(5,-4) C、(-4,-5) D、(-4,5)5. 若三角形两边长分别为3和4,第三边长是方程x2-12x+35=0的根,该三角形的周长为( )A、14 B、12 C、12或14 D、以上都不对6. 圆心在原点O,半径为5的⊙O,则P(-3,4)与⊙O的位置关系是( )
A、在⊙O内 B、在⊙O上 C、在⊙O外 D、不能确定7. 抛物线y=x2+bx+c的图象向右移2个单位长度,再向下平移3个单位长度,所得图象的解析式为y=x2-2x-3,则b,c的值为( )
A、b=2,c=0 B、b=2,c=-1 C、b=-2,c=-1 D、b=-3,c=28. 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足条件 时,⊙P与直线CD相交( )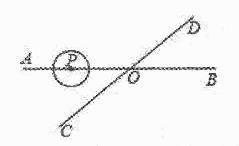 A、3≤t≤6 B、t≥6 C、t<4 D、4<t<89. 如图,⊙O是△ABC的内切圆,切点分别是D,E,F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
A、3≤t≤6 B、t≥6 C、t<4 D、4<t<89. 如图,⊙O是△ABC的内切圆,切点分别是D,E,F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )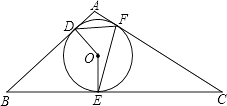 A、55° B、60° C、65° D、70°10. 如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的长为x,且0<x≤10,阴影部分的面积为y,则能反映y与X之间函数关系的大致图象是( )
A、55° B、60° C、65° D、70°10. 如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的长为x,且0<x≤10,阴影部分的面积为y,则能反映y与X之间函数关系的大致图象是( )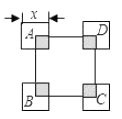 A、
A、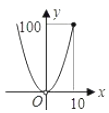 B、
B、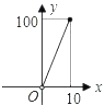 C、
C、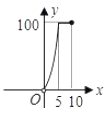 D、
D、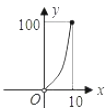
二、填空题
-
11. 若a,b是一元二次方程x2-2018x+1=0的两根,则 的值是 .
12. 一个小球被抛出后,距离地面的高度h(m)和飞行时间t(s)满足下面函数解析式:h=-5t2+10t+1,则小球距离地面的最大高度是m.
13. 如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是 .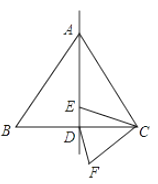 14. 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是
14. 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是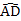 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;①②GP=GD;③点P是△ACQ的外心,其中结论正确的是 (只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;①②GP=GD;③点P是△ACQ的外心,其中结论正确的是 (只需填写序号).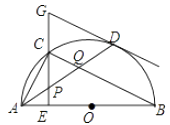 15. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:
15. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④若点A(一3,yl)、点B(- ,y2)、点C( ,y3)在该函数图象上,则yl<y3<y2;⑤若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1<-1<5<x2 . 其中正确的结论有 (只需填写序号)
三、解答题
-
16. 关于x的一元二次方程x2-(k+3)x+2k+2=0.
(1)、求证:方程总有两个实数根;
(2)、若方程有一个根小于1,求k的取值范围.
17. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)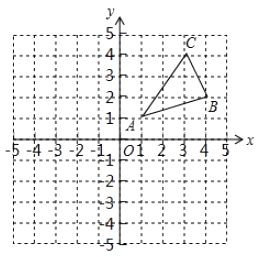 (1)、①请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(1)、①请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;②请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(2)、在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.18. 某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求w与x之间的函数关系式;
(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)、如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?19. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作: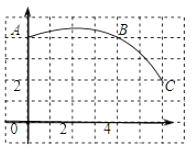 (1)、请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为;(2)、连接AD、CD,求 圆 D的半径(结果保留根号)及扇形ADC的圆心角度数;(3)、若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径(结果保留根号).20. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)、请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为;(2)、连接AD、CD,求 圆 D的半径(结果保留根号)及扇形ADC的圆心角度数;(3)、若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径(结果保留根号).20. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F. (1)、求证:CF是⊙O的切线;(2)、若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和
(1)、求证:CF是⊙O的切线;(2)、若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和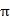 ).
).
21. 若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的”路线”.若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系。(1)、求m,n的值;(2)、当x取何值时,mx+1<x2-2x+n(3)、现将直线y=mx+1上下平移得直线y=mx+k,若直线y=mx+k与抛物线y=x2-2x+n没有交点,求k的取值范围。22. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B. (1)、求二次函数y=ax2+bx+c的解析式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
(1)、求二次函数y=ax2+bx+c的解析式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.