2017年浙江省中考数学冲刺100题(每天一练):1-10题
试卷更新日期:2017-03-24 类型:三轮冲刺
一、单选题
-
1. 下列各式计算正确的是( )A、(a+b)2=a2+b2 B、x2•x3=x6 C、x2+x3=x5 D、(a3)3=a92. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣4|,则其结果恰为2的概率是( )A、 B、 C、 D、3. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
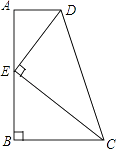 A、CE= DE B、CE= DE C、CE=3DE D、CE=2DE4. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A、CE= DE B、CE= DE C、CE=3DE D、CE=2DE4. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )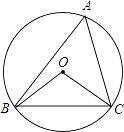 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
5. 已知点M(1,a)和点N(2,b)是一次函数y=﹣2x+1图象上的两点,则a与b的大小关系是 .6. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
 7. 如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为
7. 如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为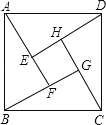
8. 如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .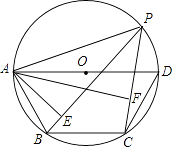
三、综合题
-
9. 已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
 (1)、求y与x的函数关系式;(2)、是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.10. 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)、求y与x的函数关系式;(2)、是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.10. 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形. (1)、若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.(2)、若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.
(1)、若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.(2)、若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.