广东省惠州市2018-2019学年九年级数学中考第一次模拟考试卷

试卷更新日期：2018-11-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的倒数是（）.

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $3$ D、 $- 3$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若x=﹣3是方程2（x﹣m）=6的解，则m的值为（）

A、6 B、﹣6 C、12 D、﹣12

查看试题解析
4. 某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：
读书时间（小时）
7
8
9
10
11
学生人数
6
10
9
8
7
则该班学生一周读书时间的中位数和众数分别是（）

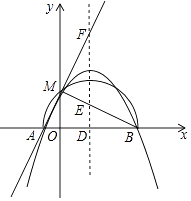
A、9，8 B、9，9 C、9.5，9 D、9.5，8

查看试题解析
5. 若分式 $\frac{x^{2} - 4}{2 x - 5}$ 的值为零，则x的值为（）

A、-2 B、2 C、±2 D、3

查看试题解析
6. 下面各组数据能判断是直角三角形的是（）

A、三边长都为2 B、三边长分别为2，3，2 C、三边长分别为13，12，5 D、三边长分别为4，5，6

查看试题解析
7. 下列每组中的两个代数式，属于同类项的是（）

A、 $\frac{1}{2} x^{2} y$ 与 $\frac{2}{3} x y^{2}$ B、0.5a²b与0.5a²c C、3abc与3ab D、 $\frac{1}{2} m^{3} n$ 与-8nm³

查看试题解析
8. ⊙O以原点为圆心，5为半径，点P的坐标为(4，2)，则点P与⊙O的位置关系是（）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、点P在⊙O上或⊙O外

查看试题解析
9. 一个三角形的两边长为3和8，第三边的长是方程x(x-9)-13(x-9)=0的根，则这个三角形的周长是（）

A、20 B、20或24 C、9和13 D、24

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ （a≠0）图象如图所示，下列结论：①abc＞0；②2a+b＝0；③当m≠1时，a+b＞ $a m^{2} + b m$ ；④a-b+c＞0；⑤若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ ，则 $x_{1} + x_{2} = 2$ ．其中正确的有（）.

A、①②③ B、②④ C、②⑤ D、②③⑤

查看试题解析

二、填空题

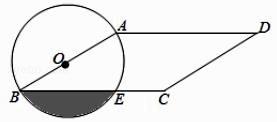
11. 在平面直角坐标系中，点A的坐标为（a，3），点B的坐标是（4，b），若点A与点B关于原点O对称，则ab= ．

查看试题解析
12. 已知一次函数 $y = k x + b$ ，其中 $k$ 从1，-2中随机取一个值， $b$ 从-1，2，3中随机取一个值，则该一次函数的图象经过一，二，三象限的概率为

查看试题解析
13. 如图，在平行四边形ABCD中，AB<AD，∠D=30°，CD=4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为．

查看试题解析
14. 如图，在△ABC中，∠A=40°，∠ABC与∠ACB的平分线相交于点P，则∠BPC的度数为.

查看试题解析
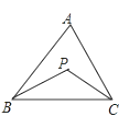15. 在平面直角坐标系xOy中，点A₁ ， A₂ ， A₃ ， …和B₁ ， B₂ ， B₃ ， …分别在直线y=kx+b和x轴上．△OA₁B₁ ， △B₁A₂B₂ ， △B₂A₃B₃ ， …都是等腰直角三角形，如果A₁（1，1），A₂（ $\frac{7}{2} ， \frac{3}{2}$ ），那么点A_n的纵坐标是．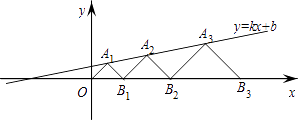

查看试题解析

三、解答题（一）

16. 计算： ${(－ 1)}^{2018} + {(－ \frac{1}{3})}^{－ 2} － {(\frac{99}{100})}^{0} + 16 \times 2^{－ 3}$

查看试题解析
17. 如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交与点G、H，若AB＝CD，求证：AG＝DH．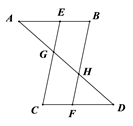

查看试题解析
18. 小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长，若已知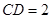，求的长．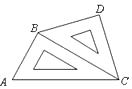

查看试题解析

四、解答题（二）

19. 如图，在 $Δ A B C$ 中， $∠ A B C = 90^{\circ}$ .

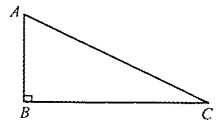(1)、作 $∠ A C B$ 的平分线交 $A B$ 边于点 $O$ ，再以点 $O$ 为圆心， $O B$ 的长为半径作 $⊙ O$ ；（要求：不写作法，保留作图痕迹）

(2)、判断（1）中 $A C$ 与 $⊙ O$ 的位置关系，直接写出结果.

查看试题解析
20. 运动对学生的成长有着深远的影响，某中学为了解学生每天运动的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．
组别
时间/时
频数/人数
频率
A
0≤t≤0.5
8
0.16
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
16
0.32
D
1.5≤t≤2
7
b
E
2≤t≤2.5
4
0.08
合计

1

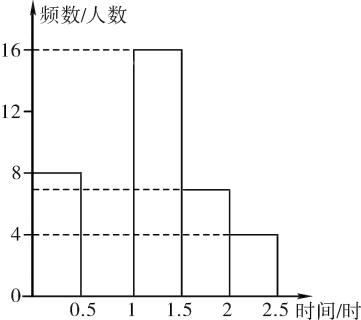
请根据图表中的信息，解答下列问题：

(1)、表中的a＝， b＝，中位数落在组，并将频数分布直方图补全；

(2)、估计该校3000名学生中，每天运动时间不足0.5小时的学生大约有多少名？

(3)、已知E组的4人中，有1名男生和3名女生，该校计划在E组学生中随机选出2人向全校同学作运动心得报告，请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率．

查看试题解析
21. 在某市实施城中村改造的过程中，“旺鑫”拆迁工程队承包了一项10000m²的拆迁工程．由于准备工作充分，实际拆迁效率比原计划提高了25%，提前2天完成了任务，请解答下列问题：

(1)、求“旺鑫”拆迁工程队现在平均每天拆迁多少m²；

(2)、为了尽量减少拆迁给市民带来的不便，在拆迁工作进行了2天后，“旺鑫”拆迁工程队的领导决定加快拆迁工作，将余下的拆迁任务在5天内完成，那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少m²？

查看试题解析

五、解答题（三）

22. 如图，在平面直角坐标系中，点O为坐标原点，直线y=﹣x+b与坐标轴交于C，D两点，直线AB与坐标轴交于A，B两点，线段OA，OC的长是方程x²﹣3x+2=0的两个根（OA＞OC）．

(1)、求点A，C的坐标；

(2)、直线AB与直线CD交于点E，若点E是线段AB的中点，反比例函数y= $\frac{k}{x}$ （k≠0）的图象的一个分支经过点E，求k的值；

(3)、在（2）的条件下，点M在直线CD上，坐标平面内是否存在点N，使以点B，E，M，N为顶点的四边形是菱形？若存在，请直接写出满足条件的点N的坐标；若不存在，请说明理由．

查看试题解析
23.
如图，AB、CD为 $⊙$ O的直径，弦AE//CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使 $∠$ PED= $∠$ C.

(1)、求证：PE是 $⊙$ O的切线；

(2)、求证：ED平分 $∠$ BEP；

(3)、若 $⊙$ O的半径为5，CF=2EF，求PD的长.

查看试题解析
24.
已知二次函数y=﹣x²+bx+c+1，
①当b=1时，求这个二次函数的对称轴的方程；
②若c=- $\frac{1}{4}$ b²﹣2b，问：b为何值时，二次函数的图象与x轴相切？
③若二次函数的图象与x轴交于点A（x₁ ， 0），B（x₂ ， 0），且x₁＜x₂ ，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足 $\frac{D E}{E F}$ = $\frac{1}{3}$ ，求二次函数的表达式．

查看试题解析

组别	时间/时	频数/人数	频率
A	0≤t≤0.5	8	0.16
B	0.5≤t≤1	a	0.3
C	1≤t≤1.5	16	0.32
D	1.5≤t≤2	7	b
E	2≤t≤2.5	4	0.08
合计			1

读书时间（小时）	7	8	9	10	11
学生人数	6	10	9	8	7