辽宁省沈阳市2019年中考数学模拟卷
试卷更新日期:2018-11-25 类型:中考模拟
一、单选题
-
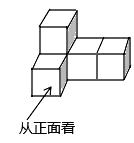
1. 下列各数是有理数的是( )A、﹣ B、 C、 D、π2. 右图是由5个大小相同的正方体搭成的几何体,这个几何体的俯视图是( )
 A、
A、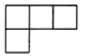 B、
B、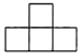 C、
C、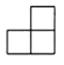 D、
D、 3. 2018年5月26日至29日,中国国际大数据产业博览会在贵州召开,“数化万物,智在融合”为年度主题.此次大会成功签约项目350余亿元.数350亿用科学记数法表示为( )A、 3.5×102 B、3.5×1010 C、3.5×1011 D、35×10104. 如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )
3. 2018年5月26日至29日,中国国际大数据产业博览会在贵州召开,“数化万物,智在融合”为年度主题.此次大会成功签约项目350余亿元.数350亿用科学记数法表示为( )A、 3.5×102 B、3.5×1010 C、3.5×1011 D、35×10104. 如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )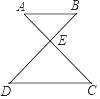 A、30° B、40° C、50° D、60°5. 下面是一位同学做的四道题①(a+b)2=a2+b2 , ②(2a2)2=-4a4 , ③a5÷a3=a2 , ④a3·a4=a12。其中做对的一道题的序号是( )
A、30° B、40° C、50° D、60°5. 下面是一位同学做的四道题①(a+b)2=a2+b2 , ②(2a2)2=-4a4 , ③a5÷a3=a2 , ④a3·a4=a12。其中做对的一道题的序号是( )
A、① B、② C、③ D、④6. 平面直角坐标系中,若点A(a,﹣b)在第三象限内,则点B(b,a)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列事件中,必然事件是 ( )A、掷一枚硬币,正面朝上. B、 是有理数,则 ≥0. C、某运动员跳高的最好成绩是20 .1米. D、从车间刚生产的产品中任意抽取一个,是次品.8. 如图,直线l是一次函数y=kx+b的图象,则其中( ) A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>09. 已知点P(1,-3)在反比例函数 (k≠0)的图象上,则k的值是( )
A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>09. 已知点P(1,-3)在反比例函数 (k≠0)的图象上,则k的值是( )
A、3 B、 C、-3 D、10. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则 的长为( )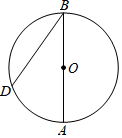 A、 B、 C、2π D、
A、 B、 C、2π D、二、填空题
-
11. 因式分解:2a2-2=.12. 在“献爱心”捐款活动中,某校7名同学的捐款数如下(单位:元):5,8,6,8,5,10,8,这组数据的众数是 .13. 化简:( + )• = .14. 学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如表,请你根据表中的数据选一人参加比赛,最适合的人选是 .
选手
甲
乙
平均数(环)
9.5
9.5
方差
0.035
0.015
15. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为实现平均每月10000元的销售利润,则这种台灯的售价应定为元.
16. 如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为。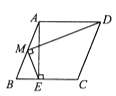
三、解答题
-
17. 计算 .18. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
 (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.19. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.19. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)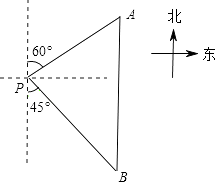 20. 在学校开展的“学习交通安全知识,争做文明中学生”主题活动月中,学校德工处随机选取了该校部分学生,对闯红灯情况进行了一次调查,调查结果有三种情况:A.从不闯红灯;B.偶尔闯红灯;C经常闯红灯.德工处将调查的数据进行了整理,并绘制了尚不完整的统计图如图,请根据相关信息,解答下列问题.
20. 在学校开展的“学习交通安全知识,争做文明中学生”主题活动月中,学校德工处随机选取了该校部分学生,对闯红灯情况进行了一次调查,调查结果有三种情况:A.从不闯红灯;B.偶尔闯红灯;C经常闯红灯.德工处将调查的数据进行了整理,并绘制了尚不完整的统计图如图,请根据相关信息,解答下列问题.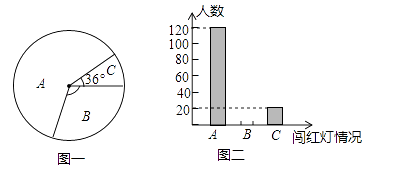 (1)、求本次活动共调查了多少名学生;
(1)、求本次活动共调查了多少名学生;
(2)、请补全(图二),并求(图一)中B区域的圆心角的度数;(3)、若该校有2400名学生,请估算该校不严格遵守信号灯指示的人数.
21. 我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际 每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货.求每月实际生产智能手机多少万部.22. 如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC , AB相交于点D , E , 连结AD . 已知∠CAD=∠B .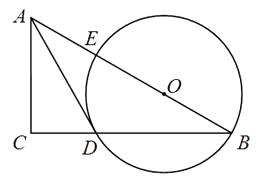 (1)、求证:AD是⊙O的切线.(2)、若BC=8,tanB= ,求⊙O的半径.23. 如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
(1)、求证:AD是⊙O的切线.(2)、若BC=8,tanB= ,求⊙O的半径.23. 如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.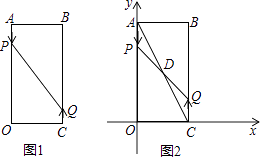 (1)、点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)、当运动时间为2s时,P、Q两点的距离为cm;(3)、请你计算出发多久时,点P和点Q之间的距离是10cm;(4)、如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.24. 在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 , , 的对应点分别为 , , .
(1)、点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)、当运动时间为2s时,P、Q两点的距离为cm;(3)、请你计算出发多久时,点P和点Q之间的距离是10cm;(4)、如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.24. 在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 , , 的对应点分别为 , , .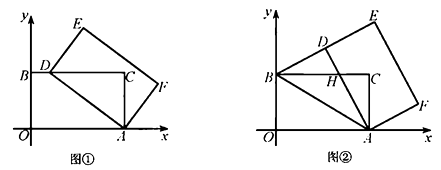 (1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .
(1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .①求证 ;
②求点 的坐标.
(3)、记 为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).25. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y轴交于点C(0,4).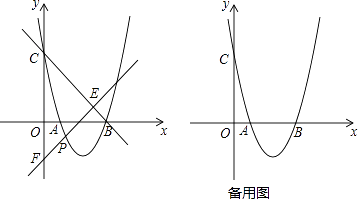 (1)、求抛物线的解析式;(2)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(1)、求抛物线的解析式;(2)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)、点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,直接写出点D的坐标;
②若△BCD是锐角三角形,直接写出点D的纵坐标n的取值范围.