北师大版九年级上期末检测卷
试卷更新日期:2018-11-24 类型:期末考试
一、单选题
-
1. 如图是由四个相同的小正方体堆成的物体,它的正视图是( )
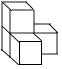 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知一元二次方程 有一个根为1,则 的值为( )A、-2 B、2 C、-4 D、43. 若点A(﹣2,3)在反比例函数 的图像上,则k的值是( )。A、﹣6 B、﹣2 C、2 D、64. 甲袋中装有2个相同的小球,分别写有数字1和2,乙袋中装有2个相同的小球,分别写有数字1和2,从两个口袋中各随机取出1个小球,取出的两个小球上都写有数字2的概率是( )A、 B、 C、 D、5. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 ,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
2. 已知一元二次方程 有一个根为1,则 的值为( )A、-2 B、2 C、-4 D、43. 若点A(﹣2,3)在反比例函数 的图像上,则k的值是( )。A、﹣6 B、﹣2 C、2 D、64. 甲袋中装有2个相同的小球,分别写有数字1和2,乙袋中装有2个相同的小球,分别写有数字1和2,从两个口袋中各随机取出1个小球,取出的两个小球上都写有数字2的概率是( )A、 B、 C、 D、5. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 ,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A、3cm B、4cm C、4.5cm D、5cm6. 下列命题中,假命题是( )A、一组对边相等的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四边相等的四边形是菱形 D、有一个角是直角的菱形是正方形7. 某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游输入将达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )A、 B、 C、 D、8. 如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
 A、1 B、 C、 D、9. 如图,矩形ABCD中,AE=BF,EF与BD相交于点G,则图中相似三角形共有( )
A、1 B、 C、 D、9. 如图,矩形ABCD中,AE=BF,EF与BD相交于点G,则图中相似三角形共有( )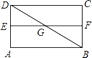 A、2对 B、4对 C、6对 D、8对10. 如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
A、2对 B、4对 C、6对 D、8对10. 如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )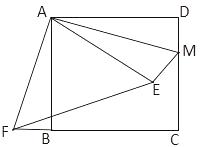 A、3 B、 C、 D、11. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )
A、3 B、 C、 D、11. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )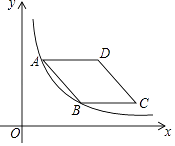 A、4 B、4 C、2 D、212. 正方形 的边长 , 为 的中点, 为 的中点, 分别与 相交于点 ,则 的长为( )
A、4 B、4 C、2 D、212. 正方形 的边长 , 为 的中点, 为 的中点, 分别与 相交于点 ,则 的长为( )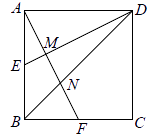 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 方程 的解是.14. 如图,在平行四边形ABCD中,添加一个条件使平行四边形ABCD是菱形.
 15. 已知点 在直线 上,也在双曲线 上,则 的值为.16. 如图,在矩形 中, ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处.下列结论正确的是. (写出所有正确结论的序号)
15. 已知点 在直线 上,也在双曲线 上,则 的值为.16. 如图,在矩形 中, ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处.下列结论正确的是. (写出所有正确结论的序号)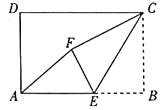
①当 为线段 中点时, ;
②当 为线段 中点时, ;
③当 三点共线时, ;
④当 三点共线时, .
三、计算题
-
17. 解下列方程:
(1)、2x2-7x+1=0(2)、x(x-3)+x-3=0.四、解答题
-
18. 经过校园某路口的行人,可能左转,也可能直行或右转.假设这三种可能性相同,现有小明和小亮两人经过该路口,请用列表法或画树状图法,求两人之中至少有一人直行的概率.
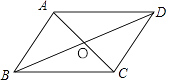
19. 如图,在正方形ABCD中,E是AB的中点,连接CE,过B作BF⊥CE交AC于F.求证:CF=2FA.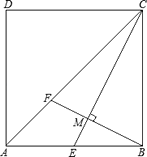 20. 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
20. 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.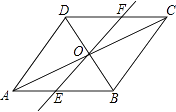 (1)、求证:OE=OF.(2)、连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.
(1)、求证:OE=OF.(2)、连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.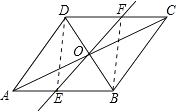 21. 列方程解应用题:
21. 列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按 元销售时,每天可销售 个;若销售单价每降低1元,每天可多售出 个.已知每个玩具的固定成本为 元,问这种玩具的销售单价为多少元时,厂家每天可获利润 元?
22.已知正方形 的对角线 , 相交于点 .
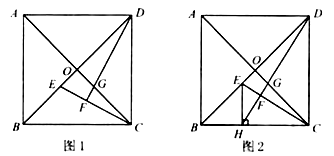 (1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
(1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,①求证: ;
②当 时,求 的长.
23. 如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC). (1)、求点A,C的坐标;(2)、直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y= (k≠0)的图象的一个分支经过点E,求k的值;(3)、在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
(1)、求点A,C的坐标;(2)、直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y= (k≠0)的图象的一个分支经过点E,求k的值;(3)、在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
-