山东省济南市市中区 2019年 高三 数学 高考模拟试卷
试卷更新日期:2018-11-23 类型:高考模拟
一、单选题
-
1. 已知命题p: x <1, ,则 为( )A、 x ≥1, B、 x <1, C、 x <1, D、 x ≥1,2. 已知 ,集合 ,若 有三个元素,则 ( )A、 B、 C、 D、3. 已知复数 对应复平面上的点 ,复数 满足 ,则 ( )
A、 B、 C、 D、4. 已知数列满足 , 且 , 则 ( )A、 B、 C、-5 D、55. 已知焦点在y轴的椭圆的离心率为 , 则m= ( )A、3或 B、3 C、 D、6. 若两直线 与 平行,则它们之间的距离为( )A、 B、 C、 D、7. 从5名男同学,3名女同学中任选4名参加体能测试,则选到的4名同学中既有男同学又有女同学的概率为( )A、 B、 C、 D、8. 已知圆 与直线 相切与点 ,点 同时从点 出发, 沿直线 匀速向右、 沿圆周按逆时针方向以相同的速率运动,当点 运动到如图所示的位置时,点 也停止运动,连接 ,则阴影部分的面积 的大小关系是( ) A、 B、 C、 D、先 ,再 ,最后9. 平行四边形ABCD中,·=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )A、 B、 C、 D、10. 已知函数 ,若对任意 ,总存在 ,使得 ,则 的取值范围是( )
A、 B、 C、 D、先 ,再 ,最后9. 平行四边形ABCD中,·=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )A、 B、 C、 D、10. 已知函数 ,若对任意 ,总存在 ,使得 ,则 的取值范围是( )
A、 B、 C、 D、11. 如图,在平面四边形ABCD中, , , , . 若点E为边CD上的动点,则 的最小值为( )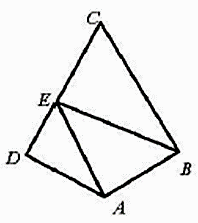 A、 B、 C、 D、12. 若曲线 的一条切线是 ,则 的最小值是( )A、2 B、 C、4 D、
A、 B、 C、 D、12. 若曲线 的一条切线是 ,则 的最小值是( )A、2 B、 C、4 D、二、填空题
-
13. 曲线 在点 处的切线方程为 .14. 已知 , ,则 .
15. 某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.16. 已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且与线段CD(包括端点C、D)有两个交点,则该双曲线的离心率的取值范围是 .三、解答题
-
17. 已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.
(Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a= , 求△ABC的面积.
18. 如图,在三棱柱 中, 平面ABC, , ,E是BC的中点. (1)、求证: ;(2)、求异面直线AE与 所成的角的大小;(3)、若G为 中点,求二面角 的正切值.19. 某工厂为了对新研发的一种产品进行合理定价,随机抽取了 个试销售数据,得到第 个销售单价 (单位:元)与销售 (单位:件)的数据资料,算得
(1)、求证: ;(2)、求异面直线AE与 所成的角的大小;(3)、若G为 中点,求二面角 的正切值.19. 某工厂为了对新研发的一种产品进行合理定价,随机抽取了 个试销售数据,得到第 个销售单价 (单位:元)与销售 (单位:件)的数据资料,算得附:回归直线方程 中, ,其中 是样本平均值.
(1)、求回归直线方程 ;(2)、预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是 元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)20. 已知抛物线C: =2px经过点p(1,2),过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B , 且直线PA交y轴于M , 直线PB交y轴于N.(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点, , ,求证: + 为定值.
21. 已知函数 。(1)、若 有三个极值点 ,求 的取值范围;(2)、若 对任意 都恒成立的 的最大值为 ,证明: 。四、选做题