2015-2016学年河南省周口市沈丘县高二下学期期中数学试卷（理科）

试卷更新日期：2017-03-23 类型：期中考试

进入出卷网下载

一、选择题

1. i是虚数单位， $\frac{5 i}{2 - i}$ =（）

A、1+2i B、﹣1﹣2i C、1﹣2i D、﹣1+2i

查看试题解析
2. 用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（）

A、假设三内角都不大于60度 B、假设三内角都大于60度 C、假设三内角至多有一个大于60度 D、假设三内角至多有两个大于60度

查看试题解析
3. 一个物体的运动方程为s=1﹣t+t²其中s的单位是米，t的单位是秒，那么物体在3秒末的瞬时速度是（）

A、7米/秒 B、6米/秒 C、5米/秒 D、8米/秒

查看试题解析
4. $\int_{2}^{4} \frac{1}{x}$ dx等于（）

A、﹣2ln2 B、2ln2 C、﹣ln2 D、ln2

查看试题解析
5. 在“近似替代”中，函数f（x）在区间[x_i ， x_i+1]上的近似值（）

A、只能是左端点的函数值f（x_i） B、只能是右端点的函数值f（x_i+1） C、可以是该区间内的任一函数值f（ξ_i）（ξ_i∈[x_i ， x_i+1]） D、以上答案均正确

查看试题解析
6. 探索以下规律：则根据规律，从2010到2012，箭头的方向依次是（）

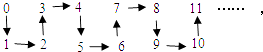A、向上再向右 B、向右再向上 C、向下再向右 D、向右再向下

查看试题解析
7. f（x），g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＜0且f（﹣1）=0则不等式f（x）g（x）＜0的解集为（　　）

A、（﹣1，0）∪（1，+∞） B、（﹣1，0）∪（0，1） C、（﹣∞，﹣1）∪（1，+∞） D、（﹣∞，﹣1）∪（0，1）

查看试题解析
8. 用数学归纳法证明“当n 为正奇数时，xⁿ+yⁿ能被x+y整除”，在第二步时，正确的证法是（）

A、假设n=k（k∈N^*），证明n=k+1命题成立 B、假设n=k（k为正奇数），证明n=k+1命题成立 C、假设n=2k+1（k∈N^*），证明n=k+1命题成立 D、假设n=k（k为正奇数），证明n=k+2命题成立

查看试题解析
9. 对于R上可导的任意函数f（x），若满足（x﹣2）f′（x）＞0，则必有（）

A、f（2）＜f（0）＜f（﹣3） B、f（﹣3）＜f（0）＜f（2） C、f（0）＜f（2）＜f（﹣3） D、f（2）＜f（﹣3）＜f（0）

查看试题解析
10. 曲线y=e^x ， y=e^﹣^x和直线x=1围成的图形面积是（）

A、e﹣e^﹣¹ B、e+e^﹣¹ C、e﹣e^﹣¹﹣2 D、e+e^﹣¹﹣2

查看试题解析
11. 点P是曲线y=x²﹣1nx上任意一点，则点P到直线y=x﹣2的距离的最小值是（）

A、1 B、 $\sqrt{2}$ C、2 D、2 $\sqrt{2}$

查看试题解析
12. 若函数 $f (x) = \frac{\sin x}{x}$ ，且0＜x₁＜x₂＜1，设 $a = \frac{\sin x_{1}}{x_{1}} ， b_{1} = \frac{\sin x_{2}}{x_{2}}$ ，则a，b的大小关系是（）

A、a＞b B、a＜b C、a=b D、b的大小关系不能确定

查看试题解析

二、填空题

13. 已知m∈R，并且 $\frac{1 + m i}{2 - i}$ 的实部和虚部相等，则m的值为．

查看试题解析
14. 观察以下三个等式：
sin²15°﹣sin²45°+sin15°cos45°=﹣ $\frac{1}{4}$ ，
sin²20°﹣sin²50°+sin20°cos50°=﹣ $\frac{1}{4}$ ，
sin²30°﹣sin²60°+sin30°cos60°=﹣ $\frac{1}{4}$ ；
猜想出一个反映一般规律的等式：．

查看试题解析
15. 若函数f（x）= $\frac{1}{3}$ x³﹣f′（1）x²+x+5，则f′（1）= ．

查看试题解析
16. 已知函数f（x）满足f（x）=f（π﹣x），且当 $x \in (\frac{π}{2} ， \frac{π}{2})$ 时，f（x）=x+sinx，设a=f（1），b=f（2），c=f（3），则a、b、c的大小关系是．

查看试题解析

三、解答题

17. 求曲线xy=1及直线y=x，y=3所围成图形的面积．

查看试题解析
18. 已知函数f（x）= $\frac{1}{3}$ x³﹣2ax²+3a²x+b（a＞0）．

(1)、当y=f（x）的极小值为1时，求b的值；

(2)、若f（x）在区间[1，2]上是减函数，求a的范围．

查看试题解析
19. 已知某家企业的生产成本z（单位：万元）和生产收入ω（单位：万元）都是产量x（单位：t）的函数，其解析式分别为：z=x³﹣18x²+75x﹣80，ω=15x

(1)、试写出该企业获得的生产利润y（单位：万元）与产量x（单位：t）之间的函数解析式；

(2)、当产量为多少时，该企业能获得最大的利润？最大利润是多少？

查看试题解析
20. 数列{a_n}中，a₁=1，S_n表示前n项和，且S_n ， S_n₊₁ ， 2S₁成等差数列．

(1)、计算S₁ ， S₂ ， S₃的值；

(2)、根据以上结果猜测S_n的表达式，并用数学归纳法证明你的猜想．

查看试题解析
21. 设函数已知函数f（x）=x³+ax²+bx+c在x=﹣ $\frac{1}{3}$ 和x=1处取得极值．

(1)、求a，b的值及其单调区间；

(2)、若对x∈[﹣1，2]不等式f（x）≤c²恒成立，求c的取值范围．

查看试题解析
22. 已知f（x）=2ax﹣ $\frac{b}{x}$ +lnx在x=1与x= $\frac{1}{2}$ 处都取得极值．
（Ⅰ）求a，b的值；
（Ⅱ）设函数g（x）=x²﹣2mx+m，若对任意的x₁∈[ $\frac{1}{2}$ ，2]，总存在x₂∈[ $\frac{1}{2}$ ，2]，使得g（x₁）≥f（x₂）﹣lnx₂ ，求实数m的取值范围．

查看试题解析