湘教版九年级上册期末数学试卷
试卷更新日期:2018-11-22 类型:期末考试
一、单选题
-
1. 已知 ,下列变形错误的是( )
A、 B、 C、 D、2. 下列方程是关于x的一元二次方程的是( )A、ax2+bx+c=0 B、x2+ =0 C、2x+c2=0 D、(x﹣2)(3x+1)=x3. 反比例函数 的图象经过点(-2,3),则该反比例函数图象在( )
A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、二象限4. 已知关于x的一元二次方程 有两个相等的实根,则k的值为( )A、 B、 C、2或3 D、 或5. 下列说法中,正确的是( )A、—个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小6. 某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?( )
A、4 B、5 C、6 D、77. 已知反比例函数 , 当时,随的增大而增大,则关于的方程的根的情况是( )A、有两个正根 B、有两个负根 C、有一个正根一个负根 D、没有实数根8. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、 B、
B、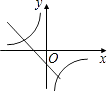 C、
C、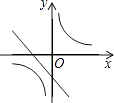 D、
D、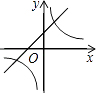 9. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
9. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( ) A、EG=4GC B、EG=3GC C、EG= GC D、EG=2GC10. 如图,已知 是 的角平分线, 是 的垂直平分线, , ,则 的长为( )
A、EG=4GC B、EG=3GC C、EG= GC D、EG=2GC10. 如图,已知 是 的角平分线, 是 的垂直平分线, , ,则 的长为( ) A、6 B、5 C、4 D、
A、6 B、5 C、4 D、二、填空题
-
11. 一元二次方程x2-3x=0的根是 .
12. 在△ABC中,若|cosA- |+(1-tanB)2=0,则∠C的度数是.
13. 某种蓄电池的电压为定值,使用此电源时,电流 与可变电阻 之间的函数关系如图所示,当用电器的电流为 时,用电器的可变电阻为 .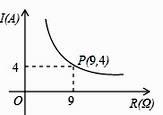 14. 如图,已知点A在反比例函数y= 上,AC⊥x轴,垂足为点C,且△AOC的面积为4,则此反比例函数的表达式为 .
14. 如图,已知点A在反比例函数y= 上,AC⊥x轴,垂足为点C,且△AOC的面积为4,则此反比例函数的表达式为 . 15. 甲、乙两名运动员进行了5次百米赛跑测试,两人的平均成绩都是13.3秒,而S甲2=3.7,S乙2=6.25,则两人中成绩较稳定的是 .
15. 甲、乙两名运动员进行了5次百米赛跑测试,两人的平均成绩都是13.3秒,而S甲2=3.7,S乙2=6.25,则两人中成绩较稳定的是 .
16. 已知线段MN的长是4cm,点P是线段MN的黄金分割点,则较长线段MP的长是cm.17. 如图,AC∥EF∥DB,若AC=8,BD=12,则EF= . 18. 如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= 米,背水坡CD的坡度i=1: (i为DF与FC的比值),则背水坡CD的坡长为米.
18. 如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= 米,背水坡CD的坡度i=1: (i为DF与FC的比值),则背水坡CD的坡长为米.
三、计算题
-
19.(1)、计算:(2)、解方程:x2-2x-1=0
四、作图题
-
20. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).

①画出△ABC关于x轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1.
五、解答题
-
21.
红岭中学在“五四青年节”组织九年级全体学生320人进行了一次“爱我中华”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如下频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
分数段(x表示分数)
频数
频率
50≤x<60
4
0.1
60≤x<70
8
b
70≤x<80
a
0.3
80≤x<90
10
0.25
90≤x<100
6
0.15
 (1)、表中a= , b= , 并补全直方图.(2)、若用扇形统计图描述此成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是;(3)、请估计该年级分数在80≤x<100的学生有多少人?22. 如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2 .求证:△ACD∽△ABC.
(1)、表中a= , b= , 并补全直方图.(2)、若用扇形统计图描述此成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是;(3)、请估计该年级分数在80≤x<100的学生有多少人?22. 如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2 .求证:△ACD∽△ABC. 23. 某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件,每件获利40元。为了迎接“六一”儿童节和扩大销售,增加利润,商场决定采取适当的降价措施,经过市场调查,发现如果每件童装每降价1元,则平均每天可多售出2件,要想平均每天在销售这种童装上获利1200元,并且尽快减少库存,那么每件童装应降价多少元?
23. 某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件,每件获利40元。为了迎接“六一”儿童节和扩大销售,增加利润,商场决定采取适当的降价措施,经过市场调查,发现如果每件童装每降价1元,则平均每天可多售出2件,要想平均每天在销售这种童装上获利1200元,并且尽快减少库存,那么每件童装应降价多少元?
24. 如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求此树CD的高. 25. 如图,A,B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB)。经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问:计划修筑的这条高等级公路会不会穿越保护区?为什么?
25. 如图,A,B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB)。经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问:计划修筑的这条高等级公路会不会穿越保护区?为什么?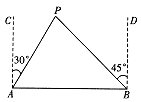 26. 已知 、 是关于 的一元二次方程 的两个实数根,其中 为非负整数,点 是一次函数 与反比例函数 的图象的交点,且 、 为常数.
26. 已知 、 是关于 的一元二次方程 的两个实数根,其中 为非负整数,点 是一次函数 与反比例函数 的图象的交点,且 、 为常数.
(1)、求 的值;(2)、求一次函数与反比例函数的解析式.
27. 如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求: (1)、当t为何值时,∠ANM=45°?
(1)、当t为何值时,∠ANM=45°?
(2)、计算四边形AMCN的面积,根据计算结果提出一个你认为合理的结论;
(3)、当t为何值时,以点M、N、A为顶点的三角形与△BCD相似?
-
-